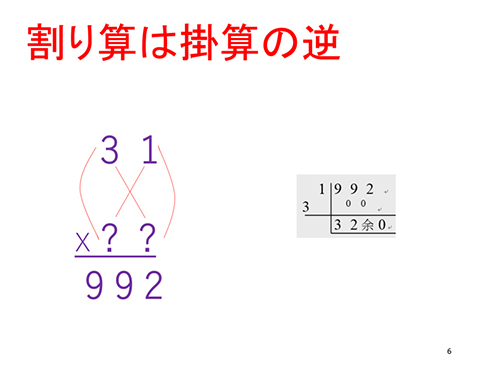
インド式計算 Step 1 まず垂直にかけ算して、そのまま数をつなげる。 一の位どうしと十の位どうしをかけ算してそのままつなげる。これで 4018 ができます。 インド式計算 Step 2 斜めにかけ算して足します。これは「たすきがけ」と言われます。 「99」の掛け算(例:99×48) – インド式 – 「11」の掛け算(例:11×34) – インド式 – 九十台同士の掛け算(例:93×91) – インド式 – 四十台同士の掛け算(例:46×48) – インド式 – 二桁の数×二桁の数(基本)(例:62×34) – つるた式 – 「hotワード#あさイチ x インド式」ツイート一覧。英語で授業、ヨガの時間あり、5歳からプログラミング、棒を使った考え方で難しい掛け算も暗算で可能インド式教育は、日本の何万歩も先に行ってるようでいいなぁー そして何か焦る💦💦

かけ算のひっさん 2けた 2けた 問題練習 Youtube
インド 式 掛け算 3 桁
インド 式 掛け算 3 桁- インド式2乗(下1桁が5の数) インド式引き算(繰り下りあり) インド式掛け算(10台の数) インド式掛け算(〜90台どうしの数) インド式掛け算(99の掛け算) インド式掛け算(基準値100) インド式掛け算(基準値0〜900) 誰でも3桁×3桁の暗算を瞬殺できるレベルになれる 落とさなければ教えられる カリキュラム ①1の位が5の時の掛け算 ②×11の場合の掛け算 ③2桁×1桁の掛け算 ④2桁の2乗 ⑤2桁×2桁の掛け算 ⑥3桁×3桁の掛け算



インド式計算 アンナ事こんな事
インド式『2桁の掛け算』19×19までの簡単な覚え方 インド式掛け算をを知っていますか? 日本では 9×9 まで暗記しますが、インドでは 19×19まで暗記をするそうです。 暗記するのもいいのですが なるべく時間をかけずに覚えたいですよね。 この方法をインド式3桁×2桁の掛け算 今度はインド式数学で、3桁×2桁の掛け算を計算してみましょう。 2桁×2桁の掛け算のやり方さえ納得できれば、3桁×2桁や3桁×3桁の掛け算も簡単です。 まずはタテ書き筆算で計算してみます。 (1)筆算のように計算式をタテ書きします。 (2)「10の位×10の位」および「1の位×1の位」を計算して書きます。 (3)「100の位×10の位」およびさて、次に、もう少し時代を進めて、ます目を使ったインド式の計算方法を紹介した。 例えば、「」なら次のように計算する。 手順1: ますの外に問題の数字を書く。 手順2: ますの中に、それぞれの積を書く。 手順3: 斜めに足す
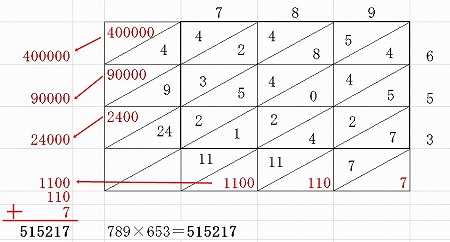
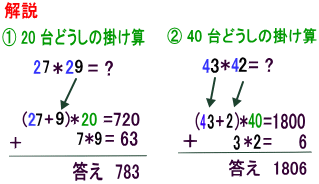
九十台同士の掛け算の暗算テクニック※ここでは、簡単に解法を紹介しています。分かりにくい方は「90台同士の掛け算(例:92×98)の暗算のコツ」をご覧ください。もう少し詳しい解説を行っています。 対象となる式の例 解き方 計算例(その一) 計算例(その二) 練習問題 アドバイ A インドはゼロ "0"という概念を生んだ国です通常学校では最低でも小学校で x 12を勉強。算数にはかなり力を入れる。インド式数学を使って、基本となる2桁×2桁の掛け算をしてみましょう。 まず筆算のようにタテに書きます。 インド式計算「3桁×3桁掛け算」 6|2716||4036| 6| 43 | 95 | 76 | + + + + 5 10 7 2
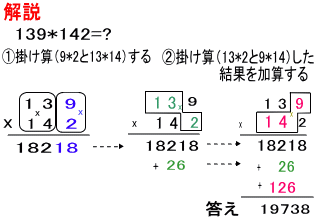
トップページ> 4掛け算> 3桁以上のインド式掛け算 3桁以上のインド式掛け算 インド式計算でも3桁以上になるといかに 効率のいい計算方法を考えるかが重要です。 まずは計算をしましょう。 275×521 2桁と1桁に分けて計算します。 計算が難しい 場合は1桁づつに分けてもいいで 3桁以上に計算をする場合、足し算と違い引き算は 気をつけないといけない事があります。 まずは3桁で説明します。 = この場合、100の位と10の位で分けて、1の位だけで 計算すると先ほどのインド式計算術が使えますが これらの掛け算は 56×54=3024 62×68=4216 33×37=1221 となり一瞬で計算ができます。なにか規則に気づきましたか?実は下2桁に注目すると、1の位同士の掛け算がそのまま現れていることがわかります。 驚きの法則ですね!では上2桁はどう計算されるのでしょう?




インド式計算で2桁のかけ算を暗算 10種類の計算法と練習問題 ドリル でトレーニング



計算名人への道 インド式計算 2 2桁 2桁の暗算 中学受験ブログ
6×10+30×1=(6+3)×10=90 つまり10の位は6+3になるわけです。 水色の部分は100の位の面積です。 30×10=300 100の位は3となります。 この3つの面積をたすと、6+90+300=396となります。 これがインド式計算術ですが、掛け算の九九さえできれば簡単にできることがお分かりいただけたと思います。 インド式2桁×2桁の掛け算 インド式掛け算の基本ルール 3ポイント インド人学校で「小2で3ケタ同士のかけ算」 まず、取り上げるのが、10月17日公開の記事 「日本でインド式教育 IT立国支える理数脳づくり」 で



インド式計算方法




インド式計算 アンナ事こんな事
上の問題の答えは,「インド式かけ算」を勉強した後に第3節で改めて解いて確認することにしましょう。 「インド式計算」とは 以下では「インド式かけ算」による2桁×2桁の計算に取り組んでいきます。次のような問題があったとしましょう。 \(47\times62= \)インド式掛け算の基本ルール (1)全部の数の組み合わせを掛け算する (2)位を間違えないように、桁を区切って(1)の答えを書く (3)(2)を足し算して答えを出す インド式:図形で解く掛け算例⇒リンク 線を引く方法のポイント 掛け算を直線の徹底解説インド式! 2桁かけ算の暗算をマスター (その1) インドでは九九のように19×19まで答えを暗記します。 これをベースにして他の計算に広げる。 たとえば、12×36=12×18×2とすれば、12×18を計算したあと2倍すれば答えが出るというように。 他にも




インド式計算 掛け算 で計算速度に革命を起こせ 3桁編 Youtube



前田の算数 インド式かけ算
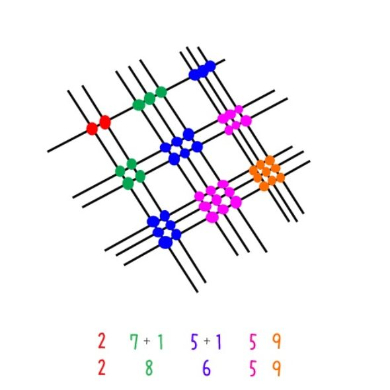
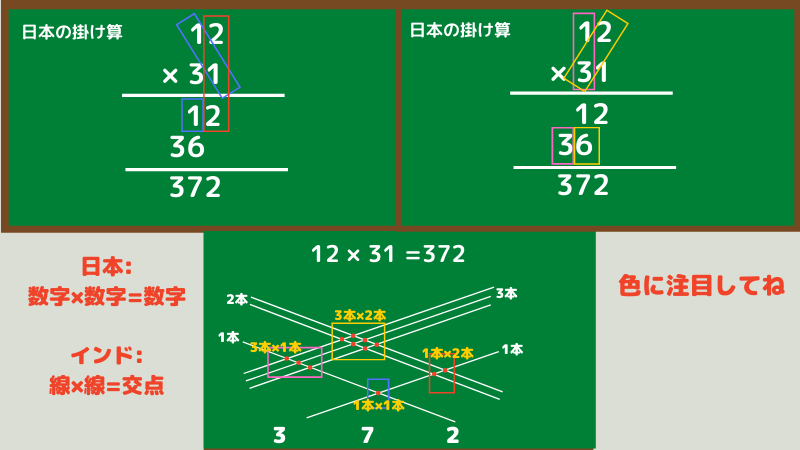
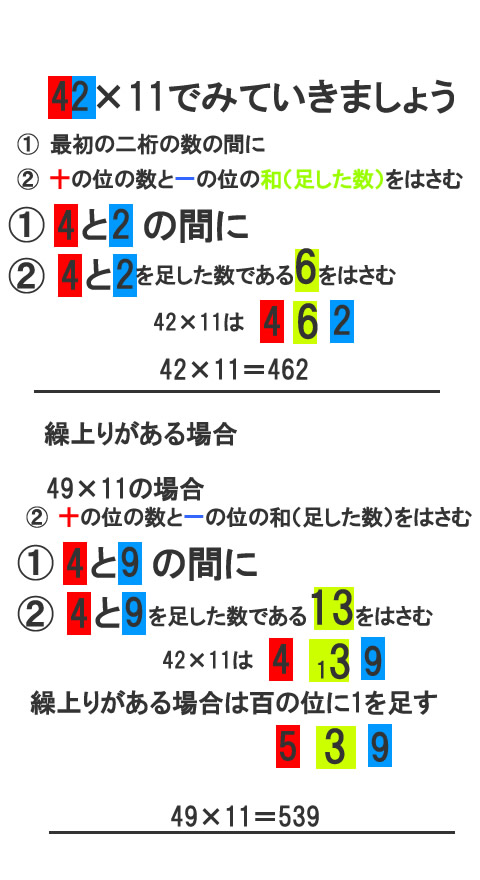
インド式掛け算で5桁掛ける3桁の計算 補足コメントしたとたんに締め切られたので再質問です。 同じ桁数の掛け算なら考え方は理解できるのですが、桁数が違う場合の計算方法がちょっとわかりません。 *678の計算方法を説明出来る方お願いします インド式2乗(下1桁が5の数) インド式引き算(繰り下りあり) インド式掛け算(10台の数) インド式掛け算(〜90台どうしの数) インド式掛け算(99の掛け算) インド式掛け算(基準値100) インド式掛け算(基準値0〜900) 2桁のかけ算が計算しやすくなる方法。 次に紹介するのはインド式かけ算の方法。 21×13= の場合は、左側の「21」から、「2」本と「1」本を右斜め上に、線を引きます。 掛け算をする右側の「13」から、「1」本と「3」本を左斜め下に、線を引く。



一瞬で解ける 最強 かけ算テク 4つ Tabi Labo



3桁以上のインド式掛け算
インド式九九一覧表1×1〜× 九九(くく)は名前の通り、1×1から9×9までの81通りのかけ算を表にしたもので、日本では通常小学2年生の授業で習います。 しかしながらインドでは、日本と異なり、 2ケタの九九(1×1~×) を小学校で習います。 地方によってはなんと 99×99 まで 習うところもあるのだとか。 「インド人は数学に強い」というのは、こんな九九さえできれば、19x19までの掛け算であれば、解法A1だけで計算可能です。 19x17 (197)x10 9x7 = 323 (解法A1) 58x58 ((5x5)8)x100 8x8 = 3364 (解法A6) Global Nav メニューを開く Global Nav メニューを閉じる 答えは以下のようになります。 ↓↓↓ (1) 103 3 / 3 2 → 106 / 09 → 103 3 / 3 2 → 106 / 09 → (2) 97 − 3 / 3 2 → 94 / 09 → 9409 97 − 3 / 3 2 → 94 / 09 → 9409 (3) ( 1 1) × 2 / 1 2 → 404 / 01 → ( 1 1) × 2 / 1 2 → 404 / 01 → (4) ( 48 − 2) ÷ 2 / 2 2 → 23 / 04 → 2304 ( 48 − 2) ÷ 2 / 2 2 → 23 / 04 → 2304




海外のかけ算暗算テクニック インド式とアメリカ式を紹介




インド式計算 掛け算 で計算速度に革命を起こせ 3桁編 Youtube
インド式の掛け算とは 線を引くだけで計算できる掛け算 です。 2桁、3桁の掛け算などでも難しく考えることなく、線を描くだけで計算することができます。 「 電卓の方が早い! 」「 筆算で解くよ! 」と思うのはわかります。 しかし、掛け算を勉強したことのない 子供でも図に当てはめるだけで掛け算ができる ようになると、算数に興味を持ってもらいやすいIPhoneスクリーンショット 説明 2桁×2桁の掛け算の速解法を学ぶためのアプリです。 最小のメモ、もしくは、暗算で計算できる解法を集録しています。 これらの解法を練習することは、良い頭の体操になります。 九九さえできれば、例えば、19x19までの掛け算であれば、解法A1だけで計算可能です。 19x17 (197)x10 9x7 = 323 (解法A1) 58x583 そのほか かけ算(掛け算)の教え方は水道方式でわかりやすく! 数学で育ちあう会 「インド式数学で計算しよう」 今まで出てきた2通りの方法で3桁×3桁までの計算を解説。




インド式 19までの二桁の掛け算は暗記なしで 暗算しよう



線を引くだけで かけ算 の答えが分かる方法がすごい ねとらぼ
3桁×3桁の掛け算公式ax|aybx|azbycx|bzcy|cz このようにインド式数学を使うことで、大きな数の掛け算もミスなく計算できるようになりました。 しかし驚くのはこれから。 インド式数学を使えば、同じ数をかける(2乗する)場合などは、もっと計算が簡単になるのです。 驚きの速さと正確さ インド式暗算とゴースト暗算 足し算引き算は3ケタまで、掛け算割り算は3ケタまでと2ケタまでの数同士で試す。3桁の数は記号を用いて書くと100a+10b+cとなります。 この式は (90+9+1)a + (9+1)b+cと変形でき、更に90×a+9×a+9×b+a+b+cという形にできます。 この変形後の式を9でまとめると9 (10×a+a+b)+a+b+cとなりますよね。



インド式掛け算 筆算 高精度計算サイト




かけ算のひっさん 2けた 2けた 問題練習 Youtube
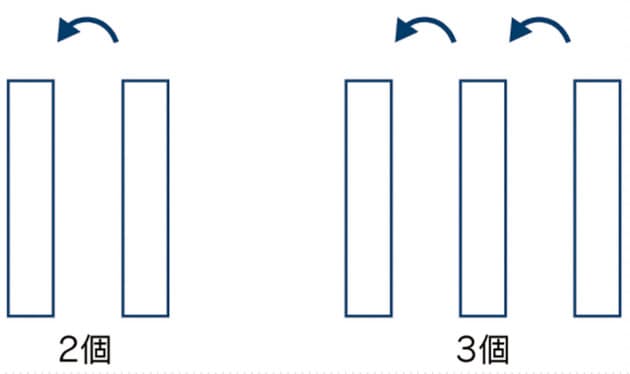
計算式とはちょっと違うが、「インド式棒算」という、これまたインドで編み出された画期的な掛け算の方法がある。 このインド式棒算 「掛け算を知らない」「九九を覚えていない」という人でも掛け算ができてしまう 、めちゃくちゃすごい計算方法なのだ。



インド式教育 3ケタかけ算 日本にも必要 Nikkei Style



小学生でもできる インド式の掛け算の計算方法




筆算型インド式数学1 Math Work Knowledge Management Math



インド式掛け算 90台どうしの数 高精度計算サイト



前田の算数 インド式かけ算



Memo インド式掛け算の仕方 Unitybox Weblog



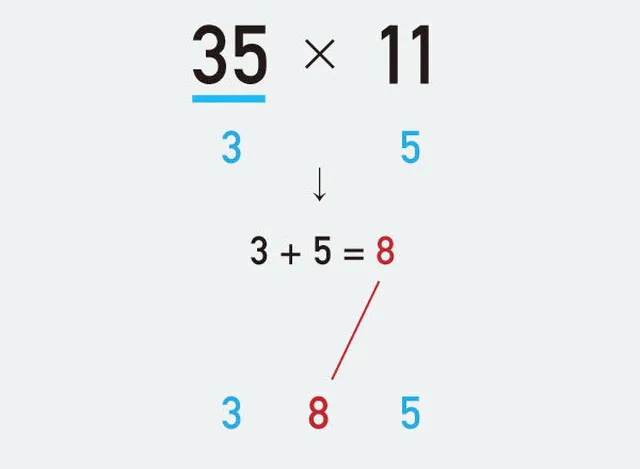
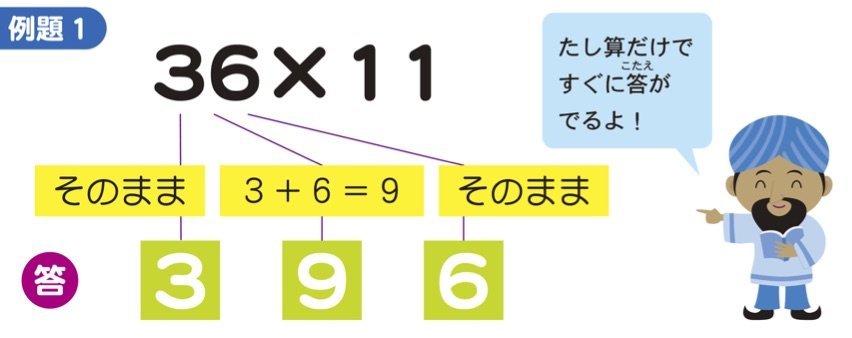
インド式かけ算を覚えよう 第三回 2桁 2桁のかけ算 2桁 11の計算 42 11など




インド式計算 掛け算 で計算速度に革命を起こせ 3桁編 Youtube



計算名人への道 インド式計算 2 2桁 2桁の暗算 中学受験ブログ
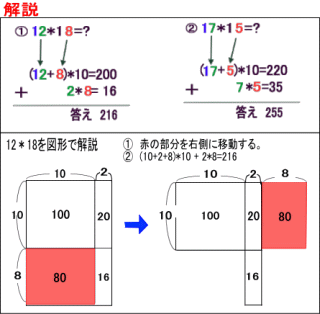



インド式掛け算 10台の数 高精度計算サイト




3桁 3桁のかけ算も暗算で 実はインドは数学がすごく得意な国だった 進路のミカタニュース




こどもプリント インド式かけ算 無料プリント かけ算 算数 暗記
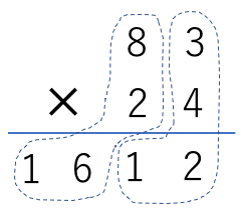



日本人もすぐ真似出来る インド式暗算 応用編 中学受験プロ講師ブログ
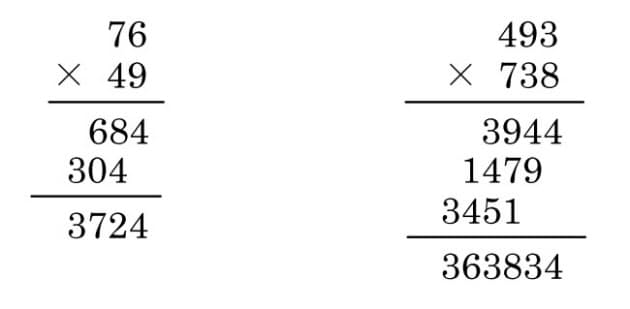



インド式教育 3ケタかけ算 日本にも必要 Nikkei Style
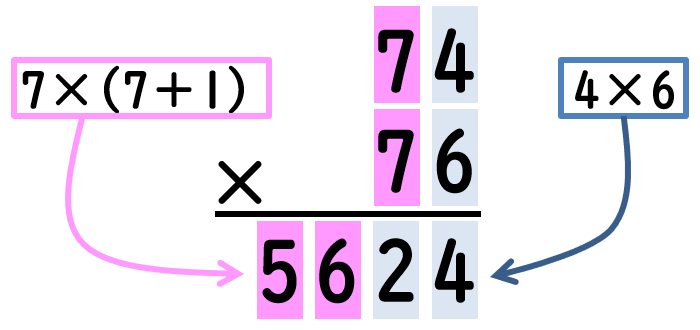



中学受験の算数成績アップに役立つインド式計算術




インド式かけ算を覚えよう 第四回 2桁 2桁のかけ算 10の台どうしのかけ算 16 14など 大学受験合格大作戦



究極の2ケタかけ算暗算法 ねこ掛け算のブログ



インド式3桁 2桁の掛け算




徹底解説インド式 2桁かけ算の暗算をマスター その1 たぶお Sapix サピックス A1 への道
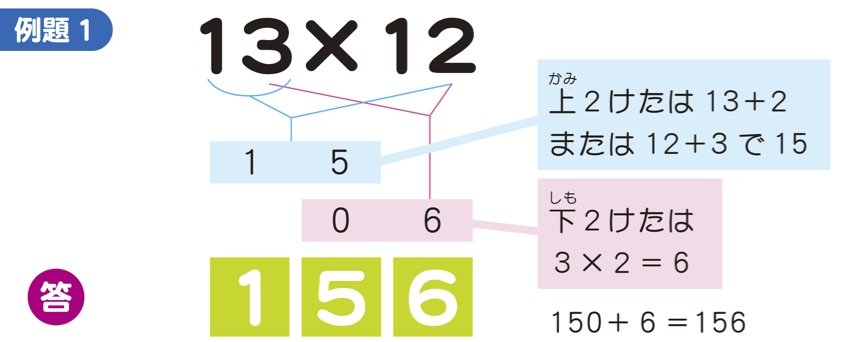



算数が楽しくなるインド式計算法 19 19がすぐ解ける 子供のインド式 かんたん 計算ドリル ダイヤモンド オンライン



3桁以上のインド式足し算



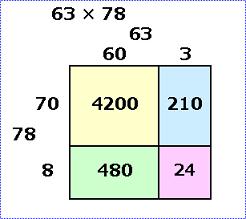
算数が楽しくなるインド式計算法 かけ算は四角形の面積で考えよう 子供のインド式 かんたん 計算ドリル ダイヤモンド オンライン



1




インド式計算11選まとめてみた かけ算わり算や19 19までの九九や足し算など 遊ぶ数学




インド式計算で1番最速で覚えやすいネタ おいしい数学



インド発の 日本式かけ算 を改良して誰でも簡単に三桁のかけ算が解ける方法を考えた Sign




小3 算数 小3 62 3けた 2けた 2けた Youtube




因数分解を使って2桁の掛け算を解く インド式計算 アーシの毎日インプット



3桁以上のインド式引き算




インド式計算ドリル 九九を卒業した人みんなに贈る魔法の計算トレーニング 中村 亨 勝久 加々美 本 通販 Amazon



インド式2桁 2桁の掛け算
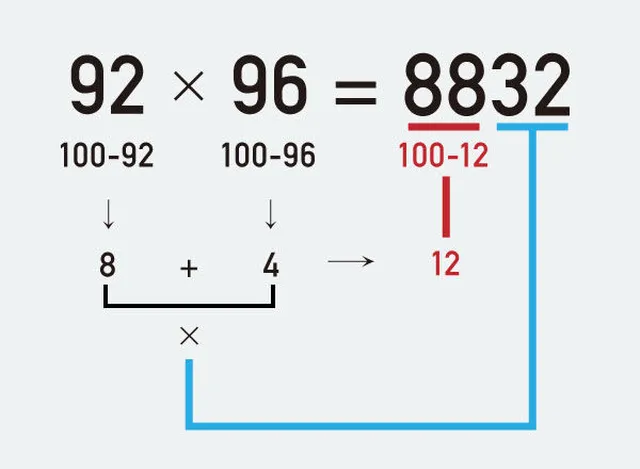



一瞬で解ける 最強 かけ算テク 4つ Tabi Labo



3



実際のところ インド式計算法 って便利なんです 本場インド人が解説したら 爆速過ぎて会場がザワザワした話 1 2 ページ ねとらぼ




インド式 3桁 3桁 算数 Youtube




第12回掲載 脳を活性化させるドリル My介護の広場




3けたのかけ算 Youtube




かけ算の筆算 Multiplication を動画でマスター インド式もあり 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



インド式教育 3ケタかけ算 日本にも必要 Nikkei Style




2桁のインド式掛け算 11 11 19 19 暗記表 無料プリント Origami Kids




筆算型インド式数学4 Teaching Multiplication Math Tricks Math Lessons




第6回 数学が苦手を克服しよう 桁の大きな掛け算 レンガ法 中学生 Tikaの勉強部屋



78 72は 2桁の掛け算を一瞬で計算できる確率を上げる方法 数学 統計教室の和から株式会社




インド式計算 掛け算 で計算速度に革命を起こせ 3桁編 Youtube




インド式かけ算を覚えよう 第五回 2桁 2桁のかけ算 和と差の積の公式が使える場合のかけ算 53 47など




早期からしっかり右脳学習で覚えるインド式かけざん 超高速の計算をマスターして世界で活躍できる子に 魔法の計算を身に付けましょう ポスト投函送料無料 Itの基礎 理数脳 インド式かけ算表ポスター 19 19かけざん インド式算数が身に付く 算数の早期学習に Acreditta Com
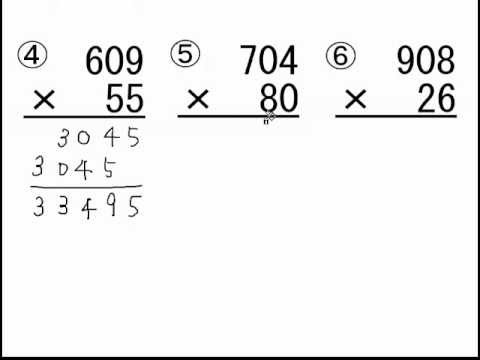



かけ算のひっさん 3けた 2けた Youtube
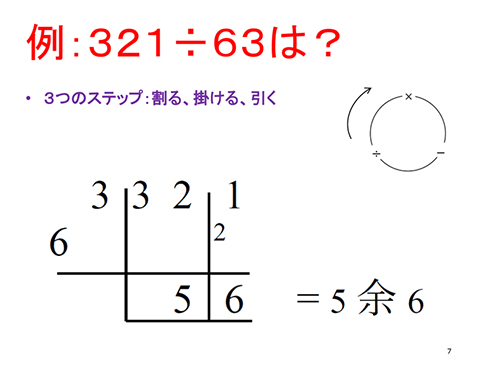



実際のところ インド式計算法 って便利なんです 本場インド人が解説したら 爆速過ぎて会場がザワザワした話 1 2 ページ ねとらぼ



前田の算数 インド式かけ算



かけ算の筆算 Multiplication を動画でマスター インド式もあり 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




目から鱗 2桁同士の掛け算を線を書くだけで簡単に計算できる方法 インド式計算 毎日を生きる そして活きる
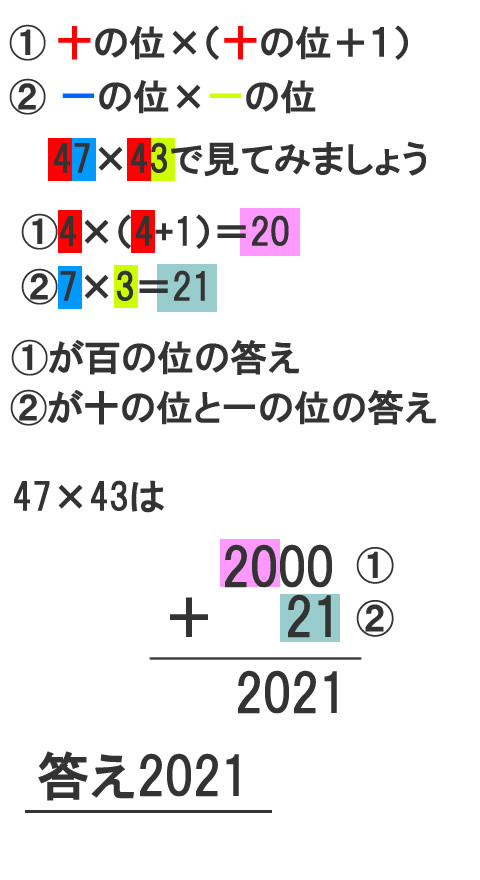



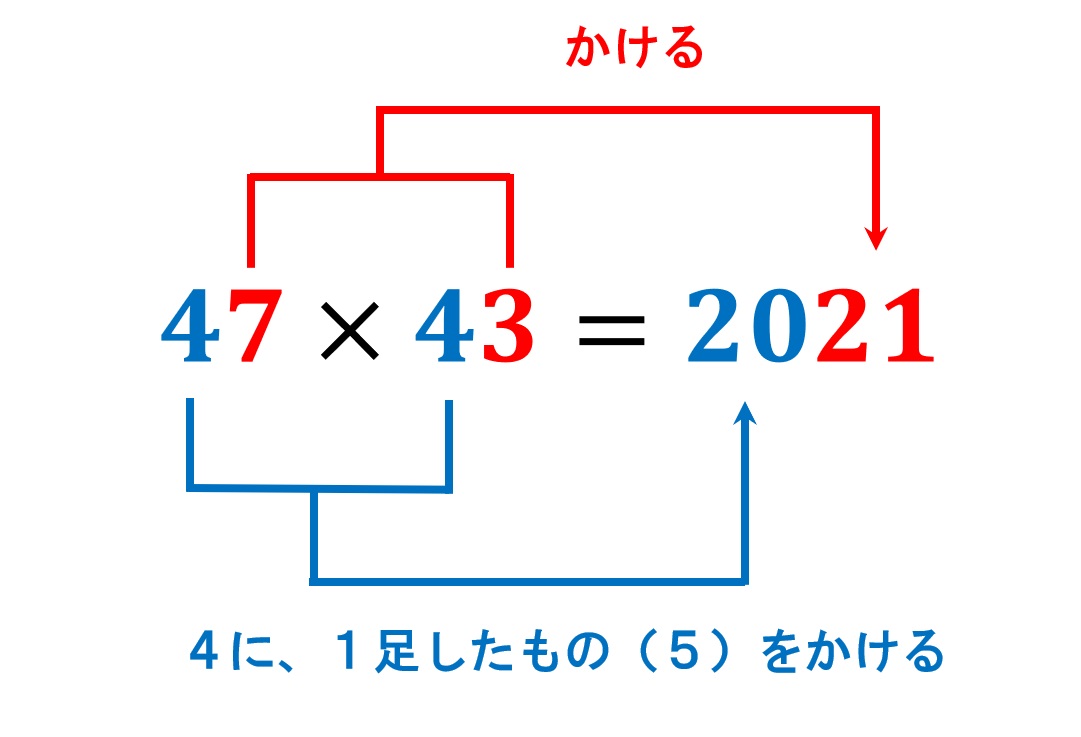
インド式かけ算を覚えよう 第二回 2桁 2桁のかけ算 十の位が同じで一の位を足すと 10 になるかけ算 47 43など
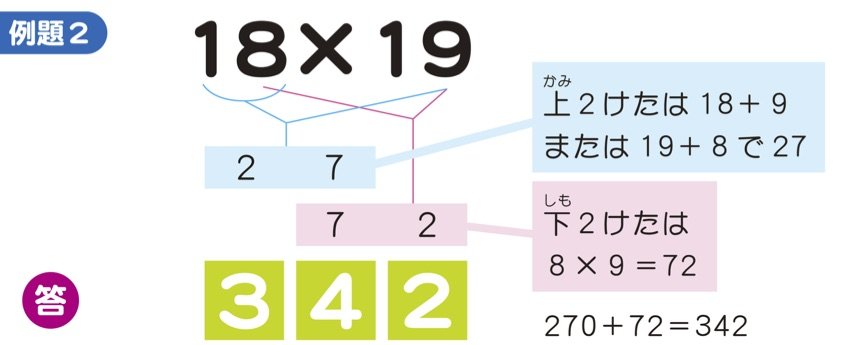



算数が楽しくなるインド式計算法 19 19がすぐ解ける 子供のインド式 かんたん 計算ドリル ダイヤモンド オンライン



前田の算数 インド式かけ算




2桁と2桁のかけ算はインド式計算が速い 53 86を2秒で計算する方法 Irohabook



インド式教育 3ケタかけ算 日本にも必要 Nikkei Style



前田の算数 インド式かけ算




インド式割り算 9で割る場合 高精度計算サイト




筆算型インド式数学3 Everyday Math Math Lessons Teaching Math
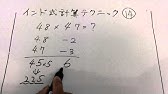



インド式計算 掛け算 で計算速度に革命を起こせ 3桁編 Youtube



インド 式 計算 インド式計算を簡単シンプルに解説します あなたも暗算の達人になれる
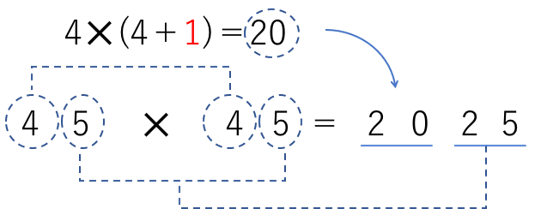



小学生も真似できる インド式暗算 中学受験プロ講師ブログ




日本人もすぐ真似出来る インド式暗算 応用編 中学受験プロ講師ブログ



1



前田の算数 インド式かけ算




日本人もすぐ真似出来る インド式暗算 応用編 中学受験プロ講師ブログ



インド式教育 3ケタかけ算 日本にも必要 Nikkei Style




インド式教育 3ケタかけ算 日本にも必要 Nikkei Style



暗算 スマイル暗算 2ケタ 2ケタ 100マス計算 99の段まで Smile暗算 インド式以外で




8 8 みたいな3桁の掛け算を簡単に計算する方法 Soutai 40



インド式教育 3ケタかけ算 日本にも必要 Nikkei Style




インド式かけ算で計算力up 2桁のかけ算もらくらくできるようになります 大学生や社会人もお勧めの暗算術です




インド式掛け算の魅力 パルメッシュを偲んで Tsuputon S Blog




インドのかけざん 線を引くだけでできるインド式掛け算 ズーノ Zoono Toys
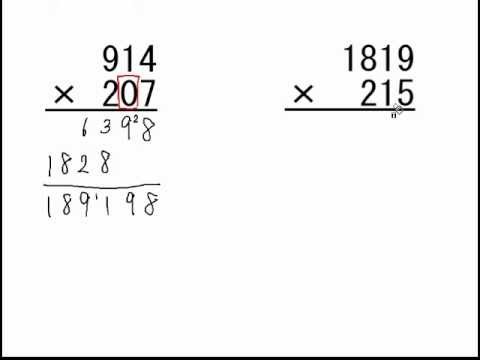



かけ算のひっさん 3けた 3けた 問題練習 Youtube




インド式計算で1番最速で覚えやすいネタ おいしい数学



九九を知らなくてもできる めざましテレビで見たインド式掛け算 あぼかどブログ




インド式2桁 2桁の掛け算 Math Tricks Mental Math Tricks Studying Math



1




インド式 3桁 2桁 質問コーナー 算数 Youtube




インド式3桁 2桁の掛け算 Math Math Equation
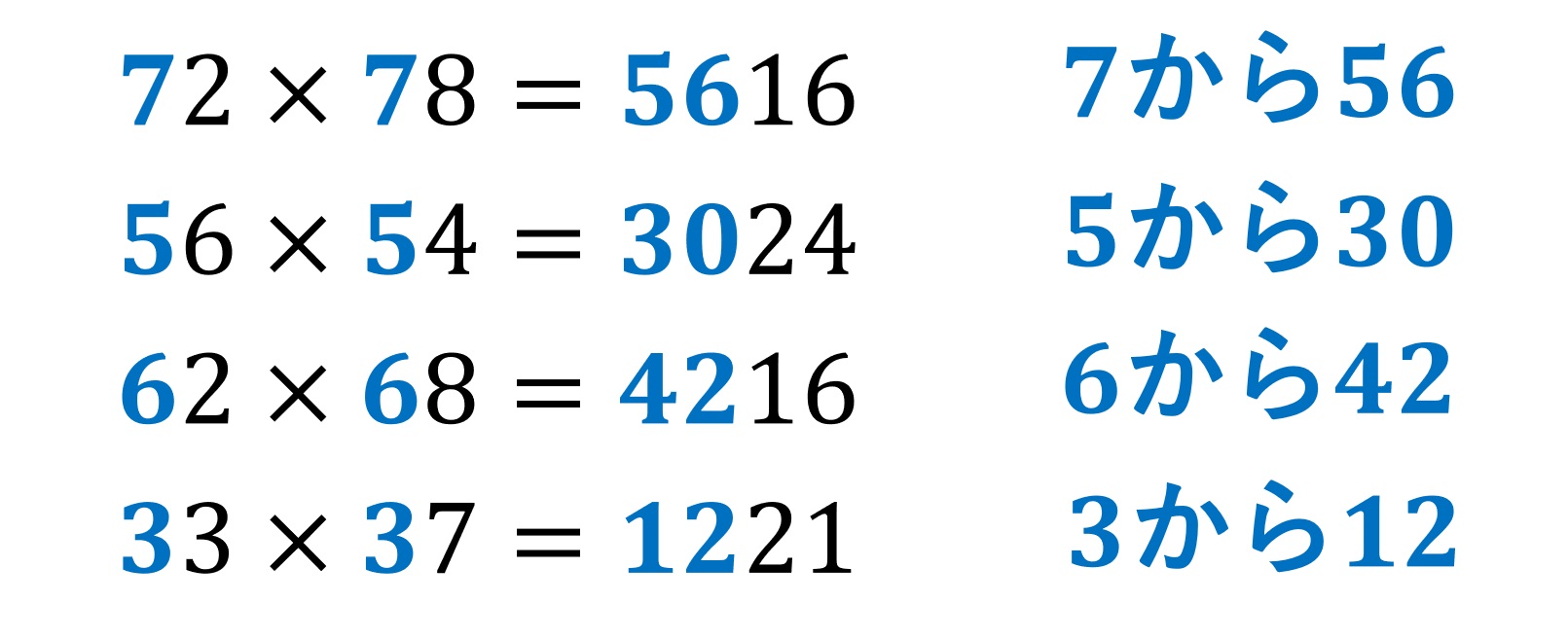



78 72は 2桁の掛け算を一瞬で計算できる確率を上げる方法 数学 統計教室の和から株式会社



実際のところ インド式計算法 って便利なんです 本場インド人が解説したら 爆速過ぎて会場がザワザワした話 1 2 ページ ねとらぼ
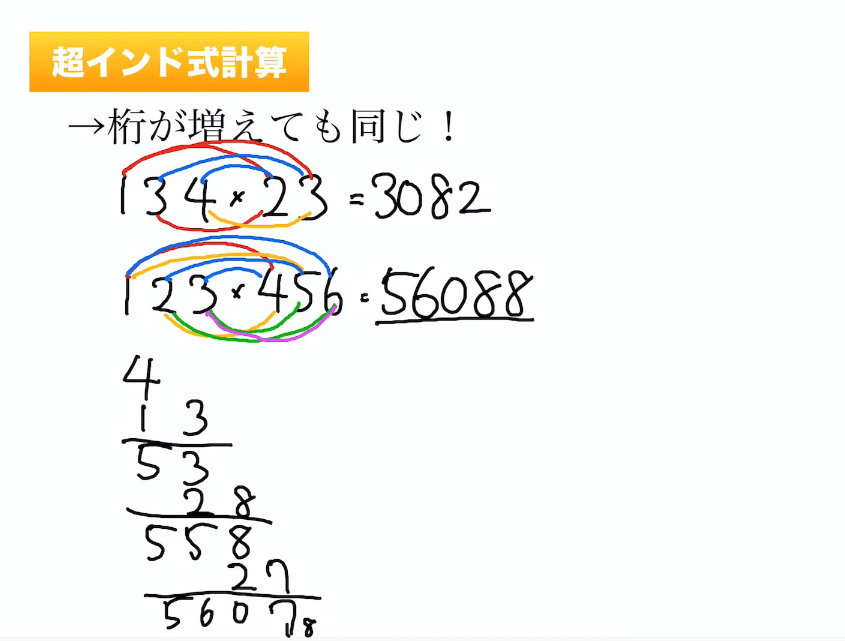



教育系youtuberから学ぶ インド式計算 の破壊力 ユースタ
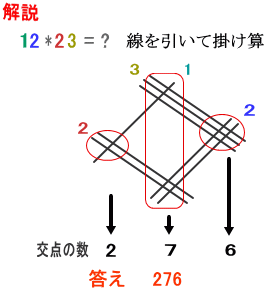



インド式掛け算 線を引いて 高精度計算サイト
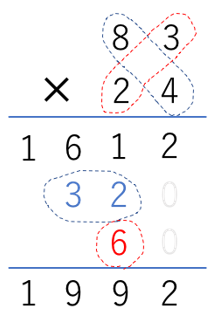



日本人もすぐ真似出来る インド式暗算 応用編 中学受験プロ講師ブログ




インド式計算 掛け算 で計算速度に革命を起こせ 3桁編 Youtube



かけ算を面白くするインド式ひっ算 中学受験プロ講師ぶろぐ
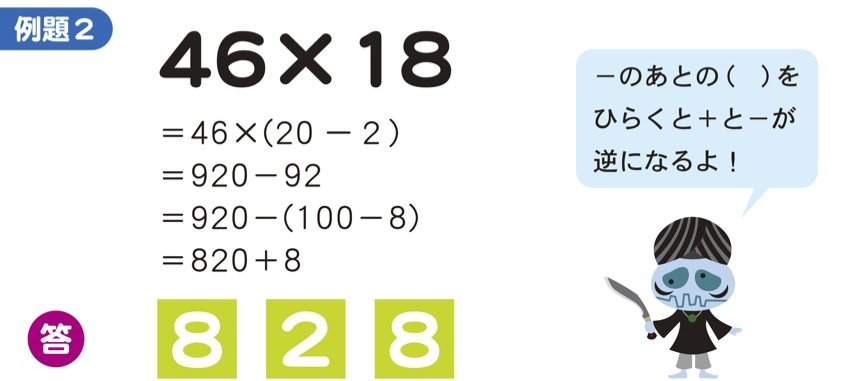



2けたの難しいかけ算も暗算で解ける秘密の方法 子供のインド式 かんたん 計算ドリル ダイヤモンド オンライン




インドのかけざん 線を引くだけでできるインド式掛け算 ズーノ Zoono Toys



0 件のコメント:
コメントを投稿