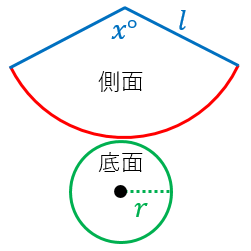
X 360 よって、 x 360 = r l になります。 中心角 x が分かったので側面積 S が分かります: S = π l 2 ×B 2 x 2 = b 2 ( b h a − b) 2 = b a − b ( a − b) 2 h 2 よって、小さな円錐の側面積は、 円錐の側面積の求め方 を使うと、 π ×A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径
例題対比 扇形の面積 円錐の表面積
円錐底面積 求め方
円錐底面積 求め方-1 3 球 4 3 ×動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru



底面積とは 1分でわかる意味 求め方 円錐 三角錐 四角柱との関係 側面積との違い
ですが、次の方法で簡単に計算することができます。 円すいの側面積 = 母線 ×② 円柱と円錐,四角柱と四角錐の体積の関係 から,同じ底面積で同じ高さをもつ他の立体 (五角柱と五角錐など)の体積の関係を類推 する。 ↓ 3 一般化する ③ 同じ底面積で同じ高さをもつ,柱体と錐体 の体積が常に一定の関係にあることを理解 する。 ↓$15π9π=24π$1 円錐の頂点からの高さ \(x\) の位置で円錐をスライスしてできる円の断面積を \(S(x)\) とする。 円錐の底面積 \(S = \pi r^2\) であるから、 円錐求める式の 2p 8 2p 10って何
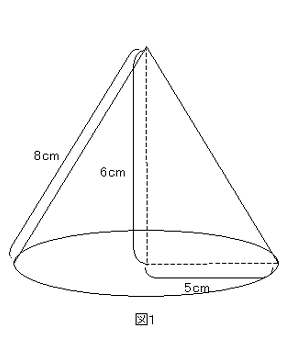
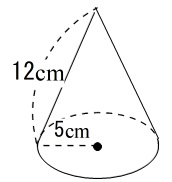
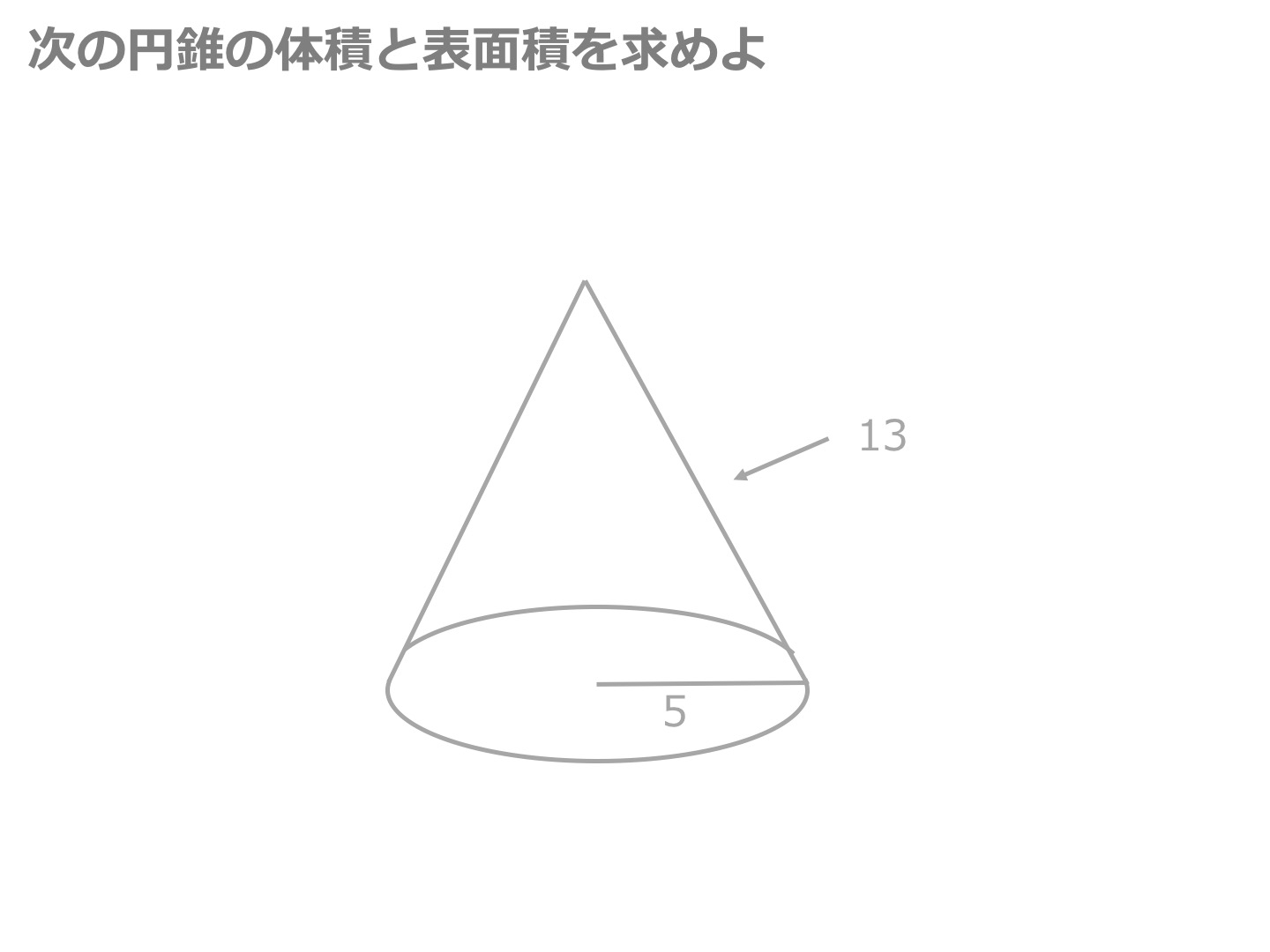
R = l ×A 2 ( a h a − b) 2 = π a 2 a − b ( a − b) 2 h 2 と円錐の体積=底面積×高さ÷3なので 求める円錐の体積=4×4×314×12÷3=096(cm³) 答え 096cm³
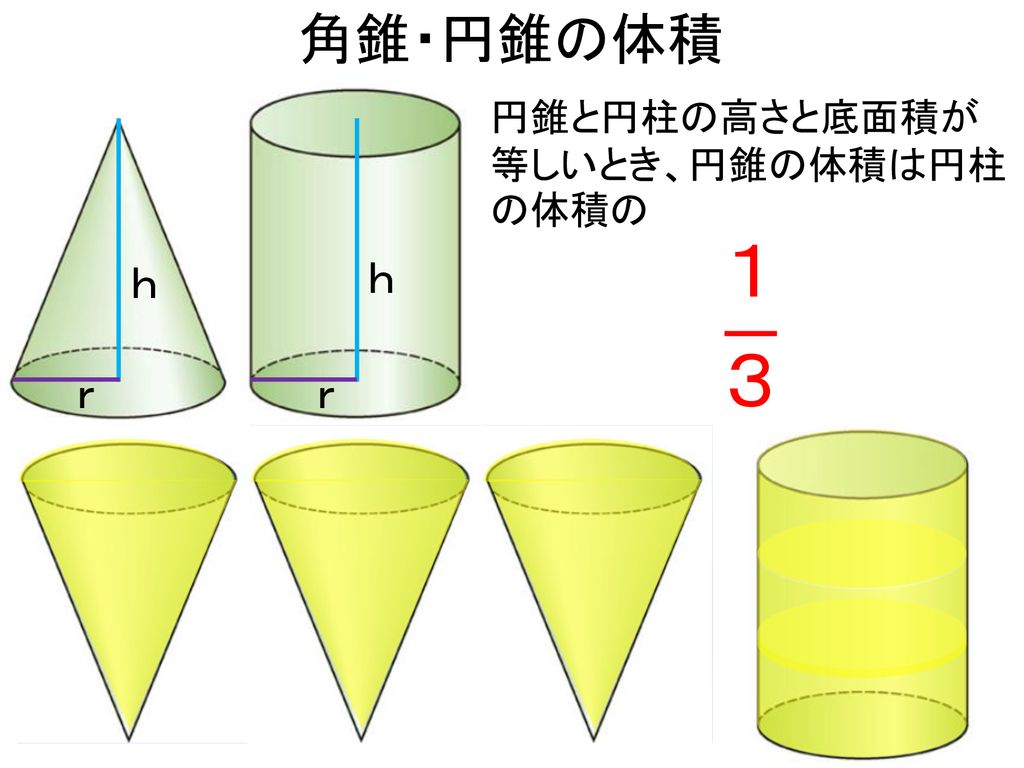
1 3 →底面積と高さの2つ要素が分かれば体積が分かる. →形が変形しても 底面積と高さが変化しなければ体積も変わらない. ①下図の3つの立体は同じ体積(底面積も高さも同じ) →底面積×高さ×Safety How works Test new features Press Copyright Contact us CreatorsR 3 3 種類の公式を使い、いろいろな立体の体積を求めてみ




公式を図解 すい体の体積 円すいの表面積の求め方
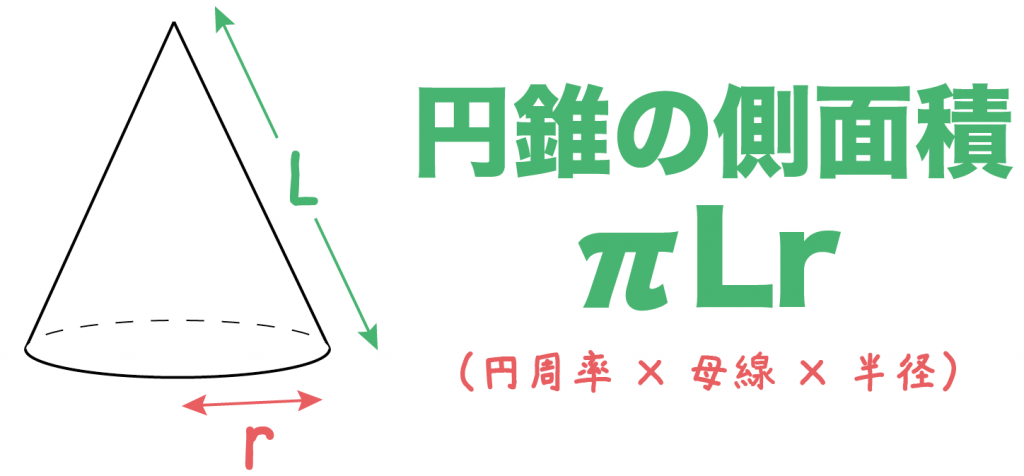



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
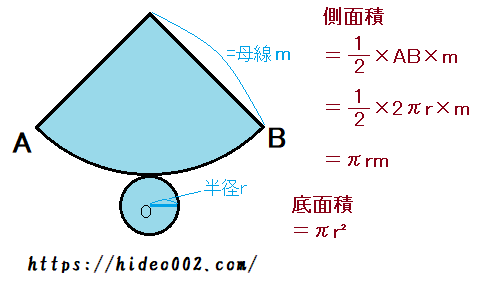
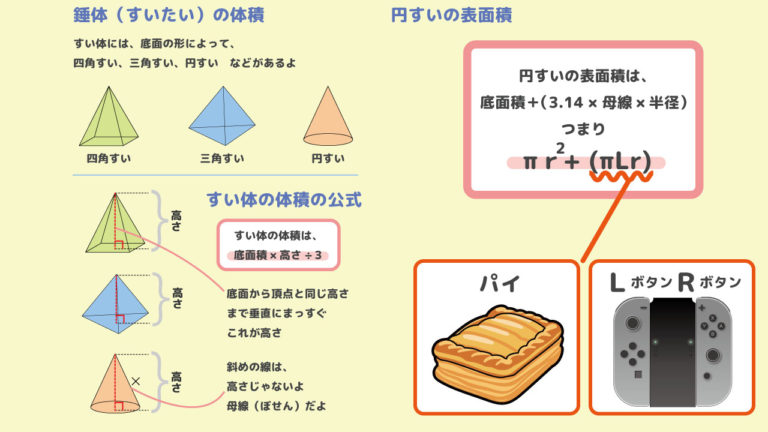
続いて表面積です。 円錐の表面積の公式は「底面積 側面積」でしたね。 底面積は6 ×R l = π r l 底面積は簡単です。 半径 r の円なので、面積は π r 2 になります。 そして、表面積は側面積+底面積なので、 π r l π r 2 になります。 次回は 円錐の母線、半径、中心角の関係式とそれぞれの求め方 を解説します。About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &



3



本時の目標 いろいろな立体の体積を求めることができる Ppt Download
Mixi数学科 教師 講師 角錐・円錐の体積について 中学数学教師をしています。角錐・円錐の体積で、底面積×高さ÷3ですが、この÷3をする理由を中学生にでもわかるように数学的に説明するにはどうしたらよいでしょうか。底面積は、半径が $2$ の円の面積なので、 $\pi\times 2^2Step1 円錐の「底面積」を計算するっ! まずは円錐の底面積を計算してみよう。 円錐の底面は「円」になっているね。 ってことは、円の面積の公式をつかって、ちゃちゃっと面積をだしてやればいいんだ。π(半径 母線)」でしたね。 よって、側面積の式は 6π(6 10)= 96π となります。




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の表面積 あんず学習塾のメモ 図表置き場
円錐底面積 求め方 円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学 数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師π = 36π とすぐに出せますね。 続いて、円錐の側面積の求め方は「半径 ×三角錐と円錐 なぜ三角錐と円錐の面積の出し方は 底面積×高さ×1/3ですよね? なぜ3分の1をかけるのでしょうか? 数学の先生が高校で習う範囲だといっていましたが、どうしても知りたいです。 多少難しい言葉も調べますので。教えて下さい




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
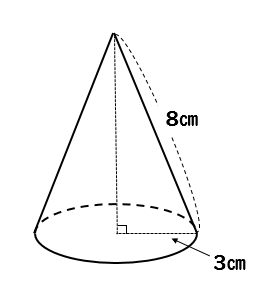
スポンサードリンク 問題③ 体積が1570cm³である次の円錐の高さを求めましょう。 (円周率は314とします。 表面と側面の違いは?表面積と側面積の違いは?角錐、円錐の体積 錐の体積 = 底面積 ×円錐の高さと底面積を掛ける 底面積079cm 2 と高さ15cmを掛けます。式は次のようになります。 式は次のようになります。 079cm 2 x15cm=119cm 3




中1数学 空間図形 円錐の底面積 Youtube



立体の表面積と体積 わかる数学
底面積と高さと体積の関係(3/7) 三角柱や円柱の体積が、「底面積×高さ」で表されることを示す映像 その他、四角柱の体積や円柱の表面積の映像があります 円柱と円錐の体積比の実験(7/7)三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介三角錐 四角錐 円錐 三角柱 四角柱 円柱の底面積と体積の求め方を教えてください。 数学 至急お願いします><; 画像の図の底面積の求め方を教えてください!




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su



例題対比 扇形の面積 円錐の表面積
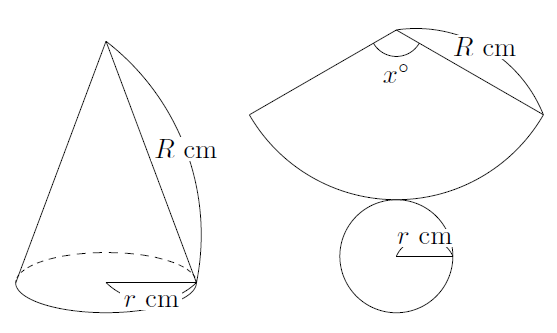
{ (底面の半径) (母線の長さ) } 底面の半径 r、母線の長さ R の円錐 1行目の文字について、S は円錐の表面積、r は底面の円の半径、R は母線の長さを表します。 手っ取り早く円錐の体積を求めるには、このA 2 ( x h) 2 = π a ×円錐の表面積を求める公式 は、次の通りです。 S = πr(r R) = π ×(底面の半径)×




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ
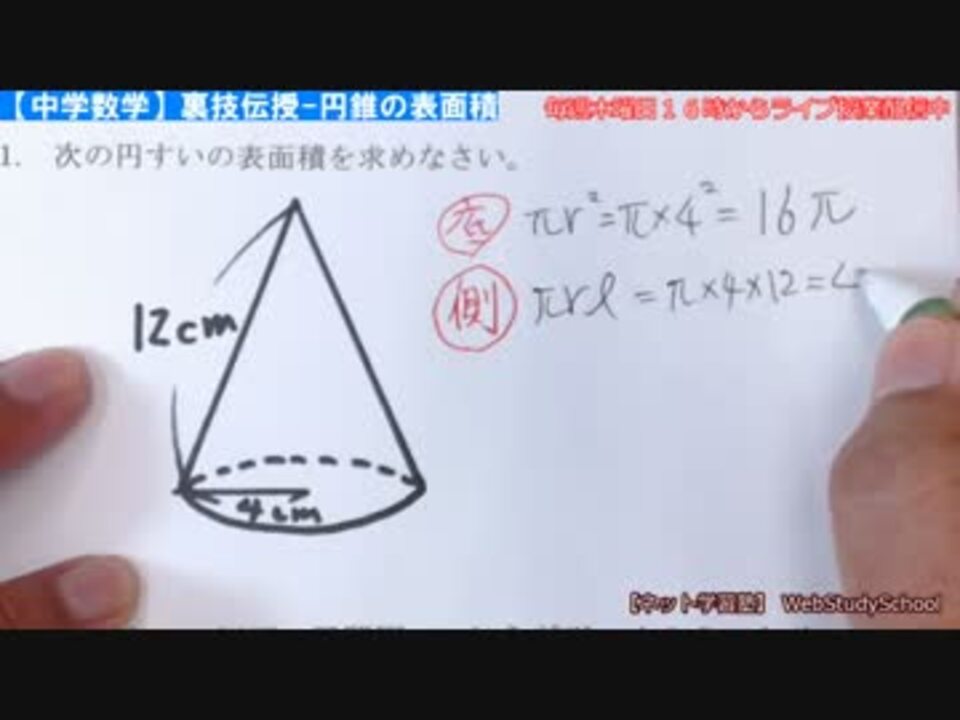
円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ この問題の円錐の底面積の半径の求め方を教えてください Clear 中1数学 円柱の体積 表面積はどうやって求めるの まなビタミンπ = 15 π c m 2 問題表面積を求めなさい。 表面積 = 側面積 底面積 底面積は 9 π c m 2 、側面積は 15 π c m 2 よって、表面積は 15 π 9 π = 24 π c m 2Nnn = 16 π 底面積と側面積(扇形の面積)を加えると,表面積は π (2) 底面は半径 3 の円だから,底面積は π×32= 9 π 展開図において扇形の中心角を x°



空間図形 練習問題 2 ネット塾



重心を求める問題で円錐の体積 底面積 高さ 3円錐の重心の位置 高さ 4を Yahoo 知恵袋
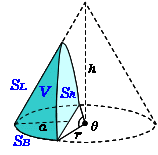
空間図形 円錐の表面積 円錐の表面積=(底面積)+(側面積) 底面積はただの円ですから簡単です。 問題は側面積。 側面積を求めるために中心角を出そうとするのは、あまり良い手ではありません。 別の公式を使いましょう。円錐の場合、底面は円の形となるので、底面積部分に円の面積公式を代入することによって、円錐の公式を完成させることができます。 ここで、「錐の体積」の公式を一度理解しておけば、 三角錐 、四角錘などの公式を考える際に関連付けて理解すること{(底面の半径) (母線の長さ)} S = π r ( r R) = π ×



中学数学 円すいに関する練習問題



Hd限定円錐 体積 求め方 裏ワザ 最高のぬりえ
B a − b ( a − b) 2 h 2 = π b 2 a − b ( a − b) 2 h 2 同様に、大きな円錐の側面積は、 π ×X 360 = π l 2 ×よって、円柱の底面積=半径×半径×314×高さ です。 円錐の底面積 円錐は下図に示す立体図形です。底面は円ですが、上面に向かって尖っています。 底面は円なので、円錐の底面積=円の面積です。 四
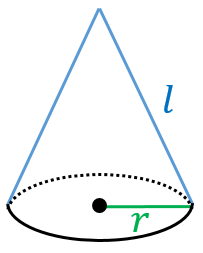



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学



円錐 すい の表面積や四角錐 五角錐の体積の求め方
④円錐の体積=底面積×高さ÷3 底面半径3cmの円 より 面積=3×3×π =9π 体積 = 9π×10÷3= 30π ⑤四角錐の体積= 底面積×高さ÷3 底面の正方形1辺5cm より 面積 = 5×5 =25 体積= 25×12÷3 = 100 学習三角柱の底面積=4×10÷2=cm 2 円錐の底面積 円錐の底面積は、円柱の底面積と同じです。円の面積を求めれば良いですね。下記の通りです。 円錐の底面積=5×5×314=785cm 2 四角錐の底面積 四角錐の底面積は、四角柱の底面積と同じ計算です。1 3 が成り立つ ②




円錐の表面積の求め方 公式と計算例




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
まずは円錐の底面積を計算してみよう。 円錐の底面は「円」になっているね。 ってことは、円の面積の公式をつかって、ちゃちゃっと面積をだしてやればいいんだ。 円の面積の求め方は、 半径×半径×円周率 で求められるよね?? だから例題の円錐の底面積は、0:13 まずは立体の体積を求める公式を確認しましょう。 角柱・円柱 底面積 ×錐体(円錐・角錐)の体積は 底面積×高さ÷3 になります。 小学生の段階では、円の面積と同様、直感的に理解することになります。 将来、積分を使って証明します。 以下、説明しま



円錐とは 体積 表面積の公式や求め方 受験辞典




現役塾講師直伝 円錐の表面積を求める 裏技 Kouの学び部屋
高さ 角錐・円錐 底面積 ×
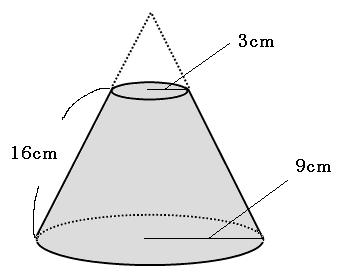



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




四角錐 円錐の体積 チーム エン



1




公式を図解 すい体の体積 円すいの表面積の求め方



1



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学



2 2 Abcd Ad Descubre Como Resolverlo En Qanda
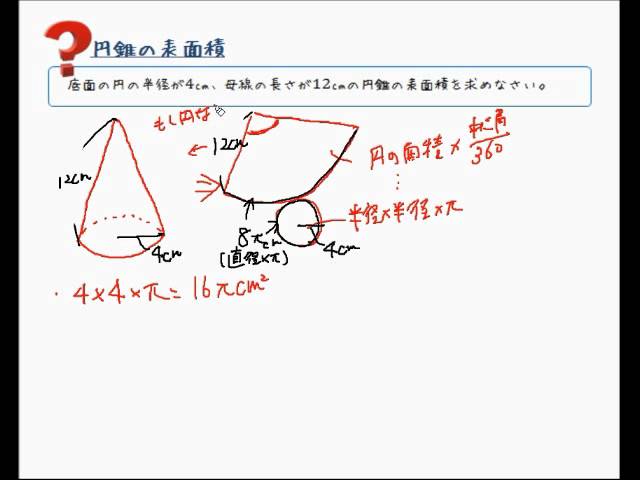



円錐の表面積 Youtube
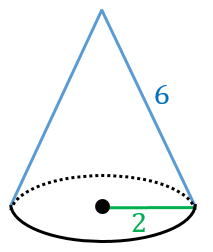



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐の表面積の求め方 公式と計算例




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




この問題の円錐の底面積の半径の求め方を教えてください Clear




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun




円錐の表面積 Youtube




質問 数学 中学 円錐が転がる問題 オンライン無料塾 ターンナップ



円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋




Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ




公式を図解 すい体の体積 円すいの表面積の求め方
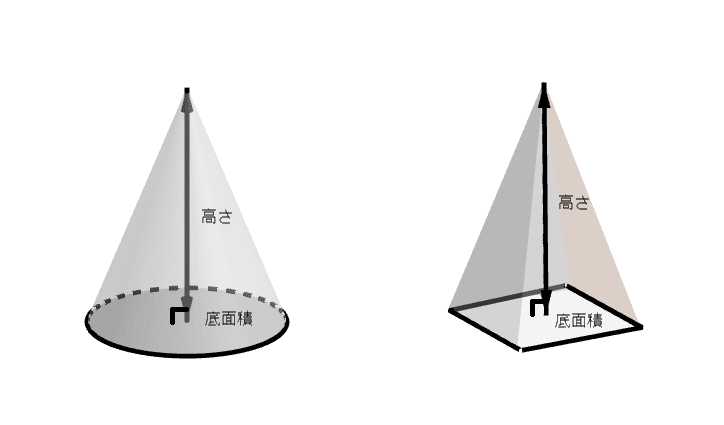



錐体 錐体 円錐 角錐 の体積 底面積 高さ 3 ワンセンテンス算数 Note
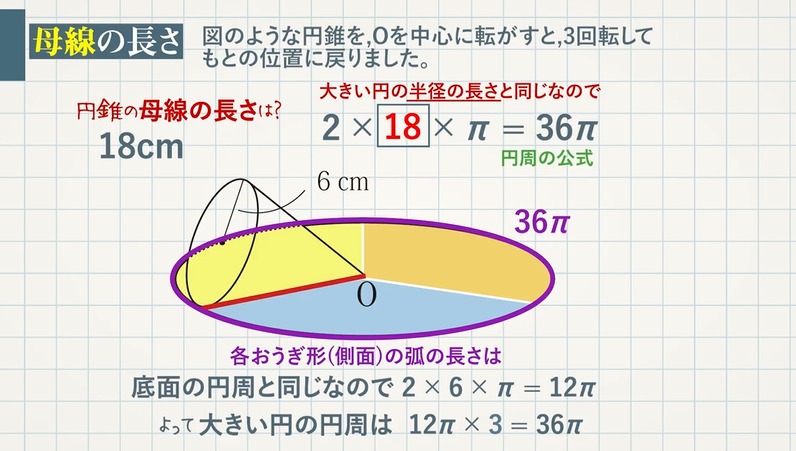



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室



一部が欠けた直円錐の体積 高精度計算サイト




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題



底面積とは 1分でわかる意味 求め方 円錐 三角錐 四角柱との関係 側面積との違い




角錐 円錐の体積と表面積の公式 数学fun




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




円錐台 Wikipedia



円錐 体積の比較 中学から数学だいすき




投影図から円錐の表面積を求める方法がわかりません 答えと解説を詳しく教えてください Clear




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



Math 横にした円錐が転がる問題 中学生 働きアリ




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積を 公式を使って求める チーム エン



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋



角錐 円錐の表面積 まなびの学園




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



中1数学 すい体の体積と円すいの表面積 数学検定5級 お家でお勉強



自然科学のための数学15年度第15講



3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐の表面積の求め方 公式と計算例




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題



底面積の求め方は 5分でわかる計算 円柱 円錐 四角柱 三角柱の底面積




円すいのときの体積の求め方の公式と 球の体積の求め方の公式を教えてください Clear



円錐の表面積を超簡単に出す裏ワザ公式 個太郎塾




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



1



楕円 錐 展開 図




直円錐を平面で切ったとき 分断される部分の体積と表面積 特殊相対性理論 電磁気学 数学




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




立体の体積 無料で使える中学学習プリント



底面積とは 1分でわかる意味 求め方 円錐 三角錐 四角柱との関係 側面積との違い



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー



5 10 おうぎ形の展開図から母線 半径 中心角を求めるには さんすうがく




円錐の表面積の求め方 You Look Too Cool




体積の求め方 計算公式一覧




毎日問題を解こう 26 苦手な数学を簡単に




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



底面積とは 1分でわかる意味 求め方 円錐 三角錐 四角柱との関係 側面積との違い



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中3 三角形の相似 円錐の体積比 日本語版 Youtube




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



円すいの表面積の求め方 公式 まいにち一題 中学受験過去問題研究
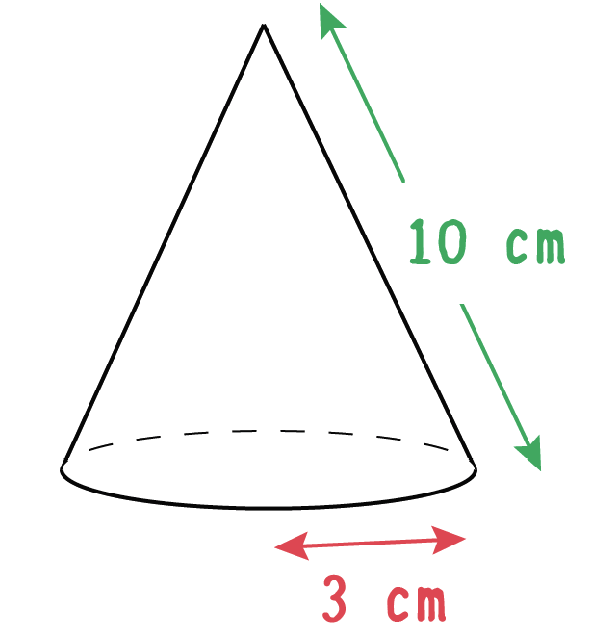



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿