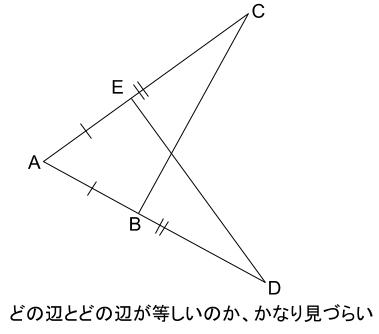
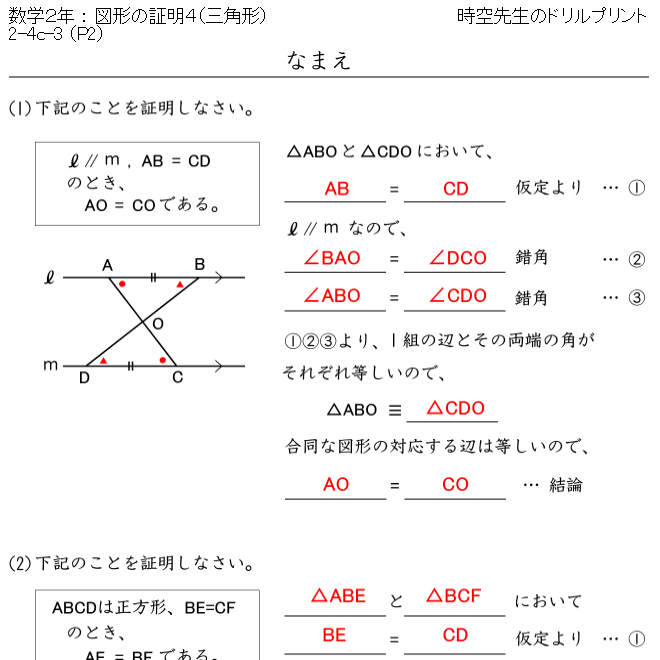
4 右の表は、四角形abcd の対角 線の性質について、まとめたもので す。 o は対角線の交点 次の各問いに答えなさい。証明は、図を書いて等しい辺や角に同じ記号をつけて考えましょう。 その他の動画は「てらtube広場」でまとめています。 てらtube広場: ht図形の証明の学習における論証の意義と考え方に関する研究 数学教育専修 千 﨑 創 都 1.研究の動機、目的、方法 中学校数学科図形領域の証明問題で次の二点で感じたことがある。
中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su
図形の証明 指導案
図形の証明 指導案-問1,問2中2の図形証明分野習った後に解ける 問3相似習った後に解ける 芸術的な難問高校入試 第52回 「平行四辺形の超難しい証明」 出典:令和3年度 都立西高校(独自作成校) 過去問 数学今回は,初心に戻って,非常に図がシンプルだけど,何かキツイ問題です。 北海道は,図がシンプルで,証明の書く量もそこまで多くないですが,何か難しい! 第27回芸術的な難問高校入試 「どの三角形」 出典:17年度 北海道 過去問: http//wwwkoukouhokkaidocedjp/gakuryokukensa/h30gakuryokuhtml 範囲:証明 難易度:★★★☆☆☆ 美し



円が2つある相似の証明問題と面積を求める問題 数学の要点まとめ 練習問題一覧
中2数学図形の証明問題を攻略できる7つのコツ 図形の証明問題のコツを知りたい! こんにちは!この記事をかいているKenだよ。コーン、最高。 図形の証明問題 ってむずかしいよね。 図形の面積を計算する問題とは ちょっと違うタイプ。 ヘロンの公式の証明と使用例 ヘロンの公式とは,三角形の3辺の長さから面積を求めるための公式です。 3辺の長さが a, b, c a, b, c a,b,c の三角形の面積 S S S は, s = a b c 2 s=\dfrac {abc} {2} s = 2a b c 証明のポイント ①条件をすべて満たしていることを示す。 ②その根拠も必ず示す。 この二つのポイントがわかっていれば、図形の証明もばっちりです。 合同の証明をしてみよう では実際に合同の証明をしてみましょう。
合同を証明してからする証明 合同な図形の性質 合同な図形の対応する角、辺はそれぞれ等しい。 この性質を利用し線分の長さや角度が等しいことを証明する。 そのためまずはじめに三角形の合同を証明する。 例2 AB=CB, AD=CDのとき ∠BAD=∠BCDを証明。 A B C D 共通 仮定を図に描きいれる。 一方証明問題では、記述によって2つの三角形が合同であることや相似であることなどを説明します。よって 数ある単元の中でも図形の証明は、異質な単元 であると言えるでしょう。 独特であるということがすなわち証明問題が難しく感じられる理由 です。図形と証明 3分なるほど!三角形の内角、外角の性質について解説! kaztastudy
Amazonで学研教育出版の中学数学 図形の証明がらくらく解ける。 (中学数学らくらく解ける。シリーズ)。アマゾンならポイント還元本が多数。学研教育出版作品ほか、お急ぎ便対象商品は当日お届けも可能。また中学数学 図形の証明がらくらく解ける。 (中学数学らくらく解ける。・三角形の角の二等分線と辺の比の証明 ・ 三角形の性質 公式 , 重心 , 外心 , 内心 , 垂心 , メネラウスの定理 , チェバの定理 , 方べきの定理 , 公式一覧 , 平面図形 , 角の二等分線と辺の比 ,追加料金は一切かかりません。 月額2,178円 (税込) で、 ①高校受験対策講座(入試本番点対策) ②定期テスト対策講座(内申点対策) ③総復習・ニガテ克服のための教科書対応した基礎講座 など 約1000を超える一流の先生の映像授業が見放題です。



Q Tbn And9gcs8jzs Zkdiyrmuisoi0mwqzez E9r9gwygbti5ixce9rlyfs0 Usqp Cau




数学 やる意味あるの あります 図形の証明問題にチャレンジ 東京 江東区猿江 住吉の少人数指導学習塾 ほっとすぺーすかたつむりのブログ 不登校 学習の遅れ 軽度発達障害にも対応
\(\triangle ABC\) が二等辺三角形であることを証明せよ 三角形が二等辺三角形であることを示したいとき、 ・\(2\) つの辺が等しい ・\(2\) つの角が等しい のどちらか片方がいえればOKです。 これ 今回は楳木敏之先生に、新刊『中学校数学科 図形の証明指導を極める』について伺いました。楳木 敏之(うめき としゆき)1968年、宮崎県生まれ。熊本大学教育学部中学校教員養成課程数学科卒業後、兵庫教育大学大学院修士課程修了。熊本県内の公立中学校合同とは \(2\) つの図形がまったく同じ形、同じ大きさであるとき、 その \(2\) つの図形は合同であるといいます。 まったく同じ形、同じ大きさ、という言葉はけっこう曖昧なので、 厳密にはもっと堅苦しい表現で合同は




図形の証明




図形を中学レベルで教えてみた
図形と証明 角度の求め方 角度の求め方 解説;内容証明 概要 一般書留郵便物の内容文書について証明するサービスです。 いつ、いかなる内容の文書を誰から誰あてに差し出されたかということを、差出人が作成した謄本によって当社が証明する制三平方の定理の証明 一辺の長さが c c の正方形ABCDがあります。 図のように、各辺の長さが a,b,c a, b, c ( c c が斜辺)の直角三角形を4つ用意し、これを正方形ABCDの各辺に合わせて一辺が a b a b の正方形PQRSを作ります。 この図形の面積を2通りの方法で出して、方程式を立てます。 「直角三角形×4」+「一辺 c c の正方形」=「一辺 a b a b の正方形」 ab 2 × 4 c2




中2数学 図形の性質と証明 1 2 二等辺三角形 1 Youtube



1
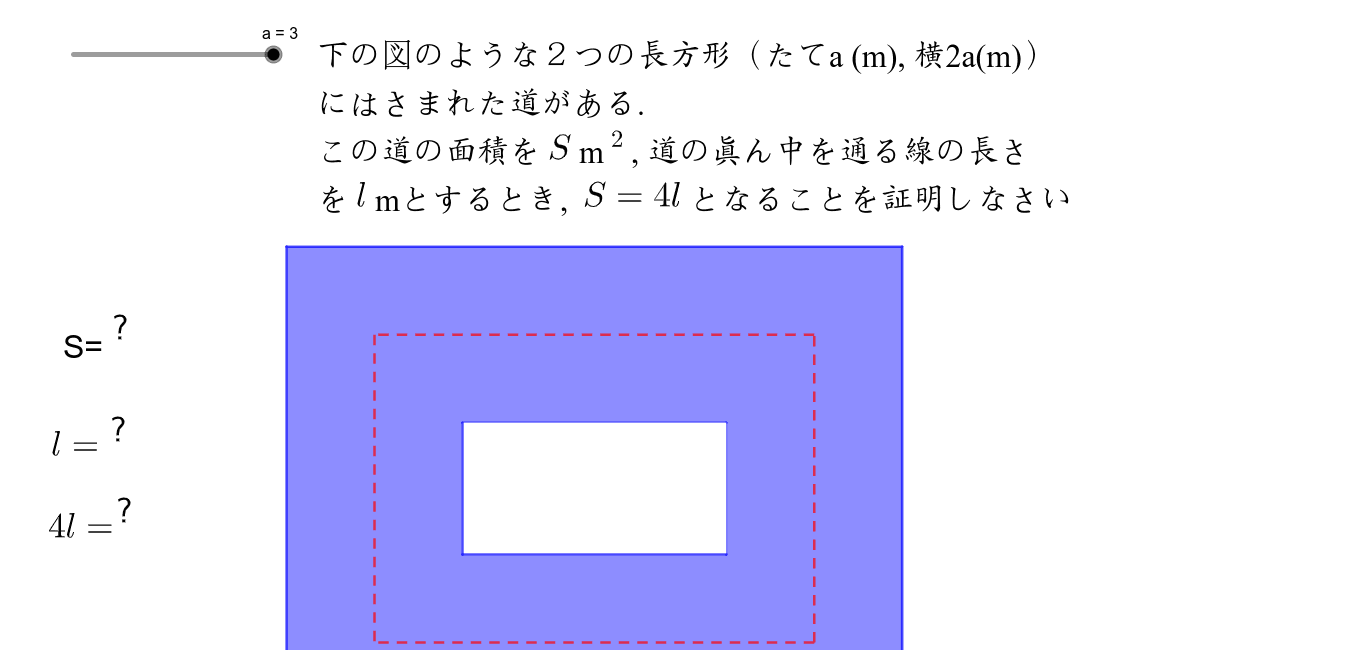
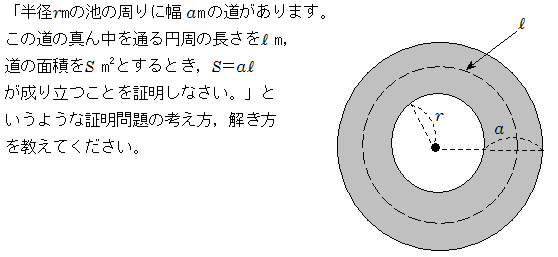
正方形の図形による証明 下の図のような2つの正方形にはさまれた幅 \(a\) mの道がある。 この道の面積を\(S\)㎡,道の真ん中を通る線の長さを\( l \) mとするとき,\(S=al \)となることを証明キーワード:図形指導(Teachinggeometry)作図(Geometricconstruction)図形の証明(Proofingeometry) 図形の性質(Propertiesofgeometricfigures) 1.はじめに 中学校数学科における図形学習では,小学校で直観的 に捉えていた図形の性質を演繹的に考えたり,小学校算図形的に面白い証明ですよね。 こういう証明を $1$ つぐらい知っておくことは大切だと思いますよ♪ スポンサーリンク 相似を用いた証明 さて、以上 $3$ つの証明が有名ですが、ここから解説する $2$ つの証明も 三角形の相似;



Ten Tokyo Shoseki Co Jp Text Chu Current Sugaku Files Thema Sugaku 09 Pdf



図形の証明 合同 現役塾講師のわかりやすい中学数学の解き方
2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。1.まず土台となる『図形の基本性質』から学習をスタート! 「図形の証明」に強くなるには、問題をただたくさんこなすことでは解決できません。 その理由は、証明問題を解くにはすべての図形の基本性質の知識が必要であるからです。 例えば、『円』と『二等辺三角形』が融合された図形では、証明の中で『円周角の性質』や『二等辺三角形の性質』がきちんと図形の対称移動と証明問題作り 福島大学人開発達文化学類 森川幾太郎 概要 中学校における幾何分野の学習では、考察対象図形の性質探しや与えられた命題の証明は生徒




中学 数学 実力テスト 過去問 平面図形と証明 問題と解答 赤城 ᐡᐤᐡ



式の計算の利用 図形の証明2 Geogebra
⇒ 証明へ 加法定理より派生する公式 2倍角の公式,3倍角の公式,半角の公式,和積の公式,積和の公式,合成公式 加法定理の図形による理解 α < 90 ° , β < 90 ° , α β < 90 ° , 0 < α − β < 90 ° の場合について図形を用いて加法定理を理解する. 和の場合2年生 5 図形の性質と証明 次の(1),(2)の各問いに答えなさい。 (1) 前の証明のまちがいは,下に示した の中にあります。まちがっている部分を, 解答用紙 の中に下線( )をひいて示しなさい。 (2) 上の証明の の中を正しく書き直しなさい。 そのためには、 図形の証明で使う最低限の知識(図形の性質、合同条件等)を頭に叩き込んで下さい。大した量ではありません。その後、「証明の書き方」を覚えます。 テンプレート化しちゃうんです。 あとは基本の証明問題を10問練習し模試レベルに移行。




三角形の合同条件と証明問題の解き方 数学fun
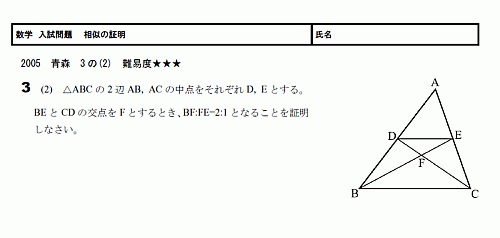



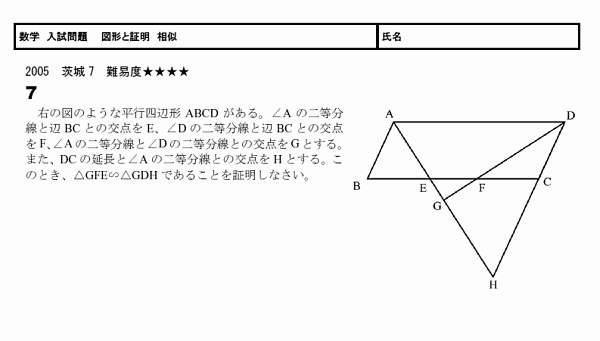
図形と証明 相似 スタディーx
中2数学 合同な図形 第6講 今回の問題はこちらです。 問題 図のように、 abcの辺bc、caをそれぞれ1辺として、三角形の外側に 正方形bdec、正方形acfgを作る。このとき、 ace≡ fcbであることを証明せよ。 "合同 第6講 解説" の 続きを読む



数学aの図形の証明問題が全くとけませんwaw 高校1年生ですコツとか Yahoo 知恵袋




円が2つある相似の証明問題と面積を求める問題 数学の要点まとめ 練習問題一覧




中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su



Studydoctor図形の性質と相似の証明 中3数学 Studydoctor




中学数学が秒でわかる 正三角形の中に正三角形がある図形の証明 超 解説付き なぜか分かる はかせちゃんの怪しい研究室




中3数学 図形と相似9 相似条件と証明 折り返しの図形 すべて無料 星組の中学数学講座



入試対策 図形の証明問題は意外と簡単だ 駿英式 勉強術



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく



19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




19年2月25日 数学 図形の証明問題 オンライン家庭教師 ウェブリー



中3数学12 図形の相似2 相似条件と証明 基本解説プリント 問題 327




無料 中2数学 基本解説 問題プリント 226 図形6 証明のしくみと根拠




Paypayフリマ かずお式中学数学ノート 中2 図形と証明



合同な図形の証明練習 個人塾 個人指導の教材




メルカリ 中学数学 図形の証明がらくらく解ける 参考書 444 中古や未使用のフリマ



接線と円と合同の証明問題 数学の要点まとめ 練習問題一覧



式の計算 式による図形の証明問題の解き方のコツ 中学数学 定期テスト対策サイト




中学数学 証明は簡単 合同な図形を探すたった1つのポイント 烈志塾 塾長ブログ



図形の証明の考え方 数学 苦手解決q A 進研ゼミ高校講座



証明の書き方 合同な三角形の証明問題のかき方を基礎から解説 数スタ




図形に関する性質の証明 身勝手な主張



図形と証明 相似 無料学習プリント教材




メルカリ 中学 数学 図形の証明がらくらく解ける 参考書 300 中古や未使用のフリマ




図形の証明のにがてな人へ 理社出版編集部 本 通販 Amazon
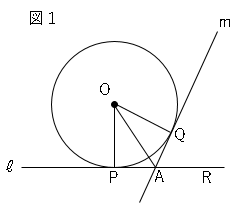



接線と円と合同の証明問題 数学の要点まとめ 練習問題一覧




14年前期 千葉県公立高校入試 数学 第4問 図形の証明 配点15点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
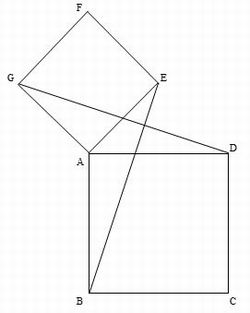



入試対策 図形の証明問題は意外と簡単だ 駿英式 勉強術




図形の証明問題を教える工夫



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に



中2数学 発展問題プリント12 図形6 証明のしくみと根拠 問題 226




中学数学 相似な図形の証明問題のコツ ちょい難問 なぜか分かる はかせちゃんの怪しい研究室



1




18年千葉県公立高校入試 前期 数学第4問 図形の証明 問題 解答 解説 18年2月13日実施 船橋市議会議員 朝倉幹晴公式サイト




高校数学 中線定理の5通りの証明 図形を扱う5分野の解法比較 受験の月



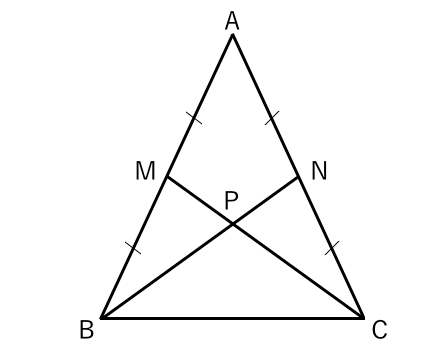
中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾
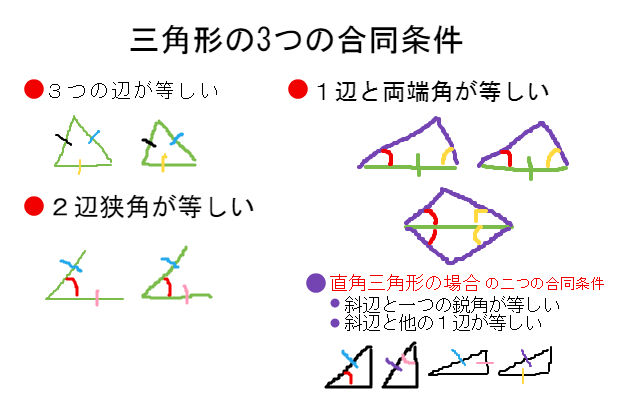



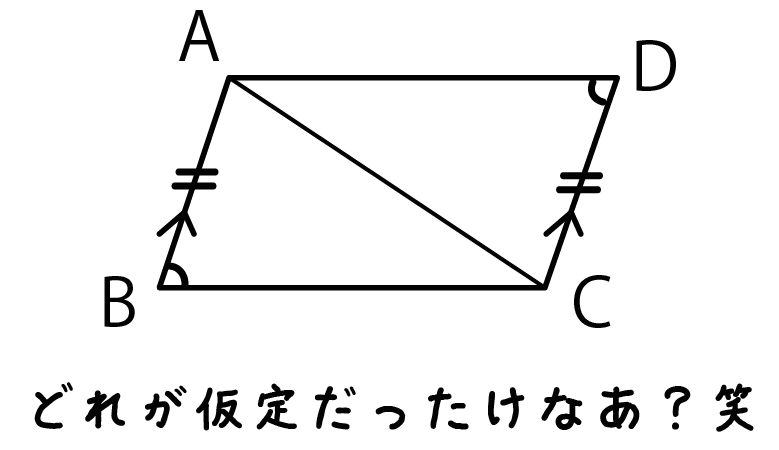
図形の証明問題に必要な最低限の知識 中学数学 理科 寺子屋塾の復習サイト




Ab Abcdfrac12abtimesce Descubre Como Resolverlo En Qanda
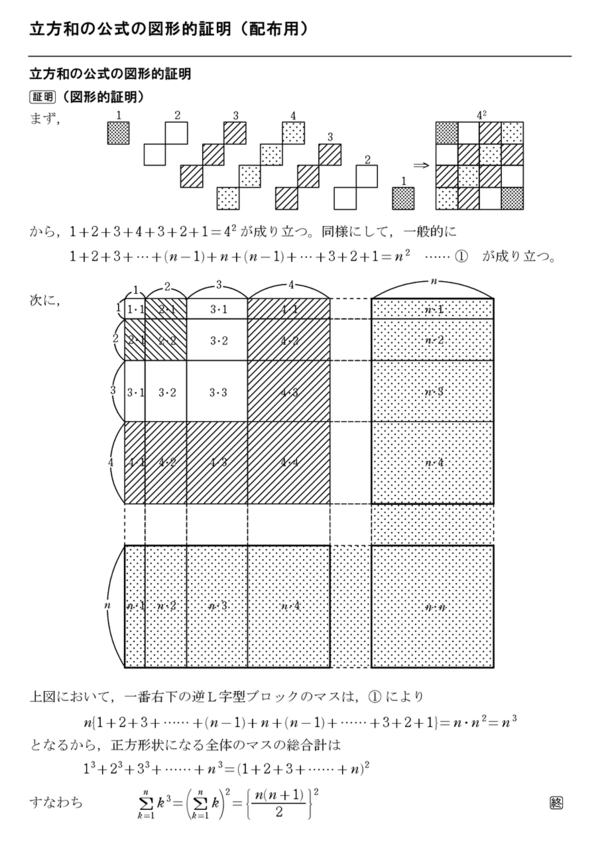



立方和の公式の図形的証明 配布用 怜悧玲瓏 高校数学を天空から俯瞰する




この様な中学二年生で習う 応用問題である証明問題での質問です この証明問題は Clear




ベクトルを使った図形の証明問題 1 ゼロからわかるベクトル第19回 Youtube




中学数学図形の証明がらくらく解ける の通販 紙の本 Honto本の通販ストア



合同な図形 三角形の証明問題 苦手な数学を簡単に




中2数学 図形の調べ方 中学生 数学のノート Clear



図形の総合問題の解き方 合同証明 三平方の定理 相似など 現役塾講師のわかりやすい中学数学の解き方



16年前期 千葉県公立高校入試 数学 第4問 図形の証明 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




ม 2 โน ตของ 数学 中2 図形の性質と証明 ช น Junior Clear




中学数学 図形の合同 図形の性質




都立入試 数学 図形の証明問題 大問4問2 図形の相似のひみつ 都立高校入試で成功する方法



新中学3年生向け 図形の証明 第1講 三角形の合同条件の利用 Youtube




メルカリ 中学数学図形の証明がらくらく解ける 参考書 399 中古や未使用のフリマ




名学館放出東校 中3 数学 式の展開や因数分解を利用した 図形問題s Al の証明問題の解説その2 Youtube




図形の証明 朝倉 幹晴 本 通販 Amazon
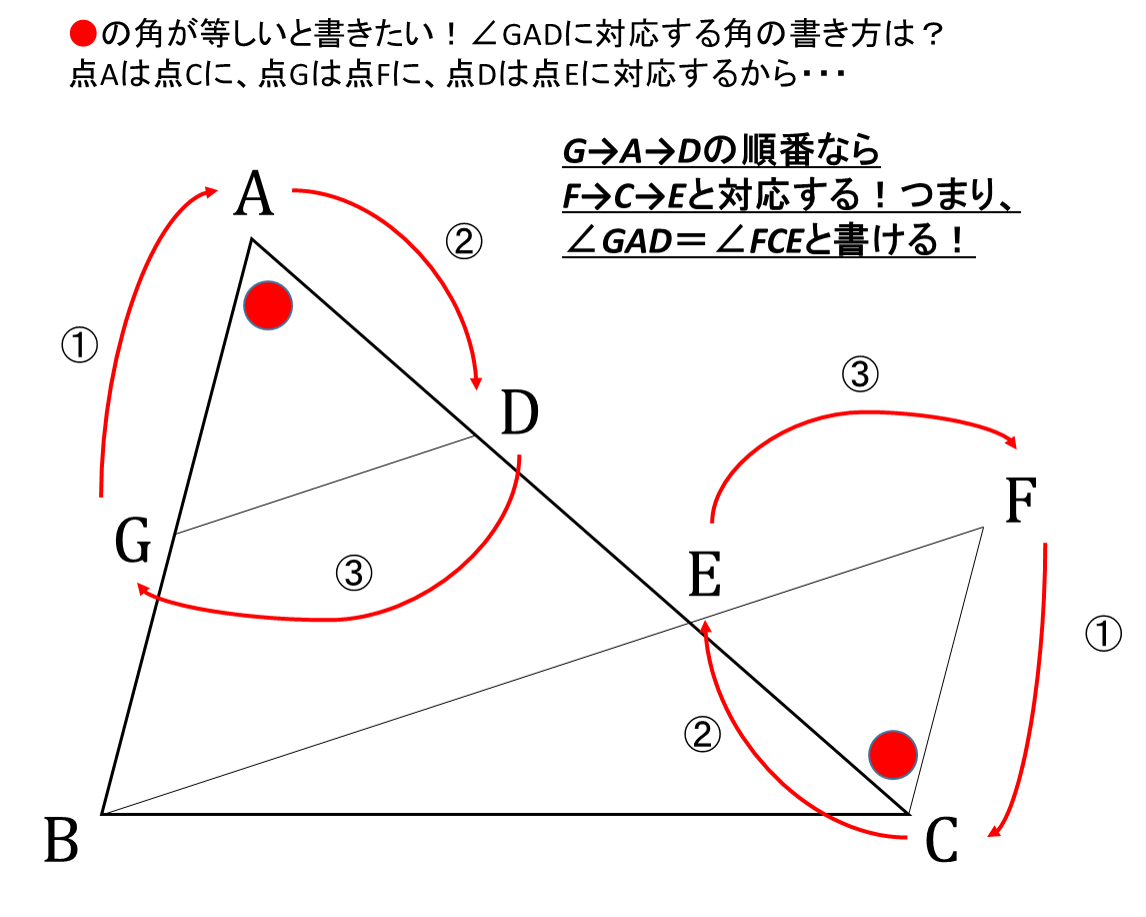



数学 中学証明問題を解く4つのポイント
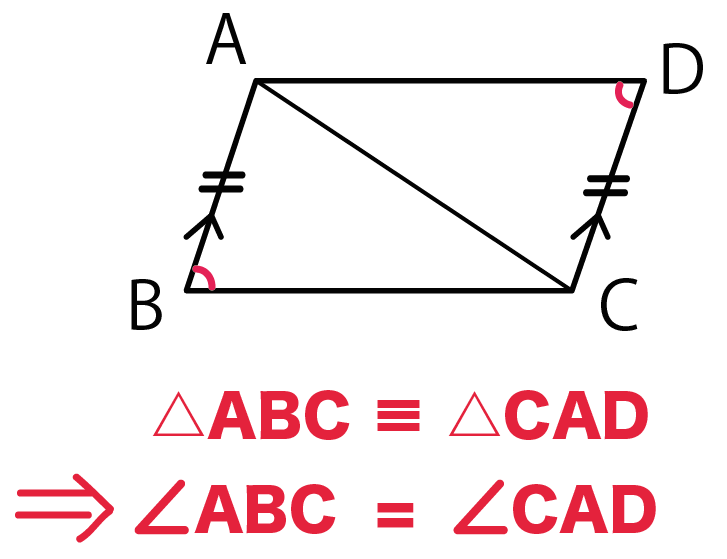



中2数学 図形の証明問題を攻略できる7つのコツ Qikeru 学びを楽しくわかりやすく
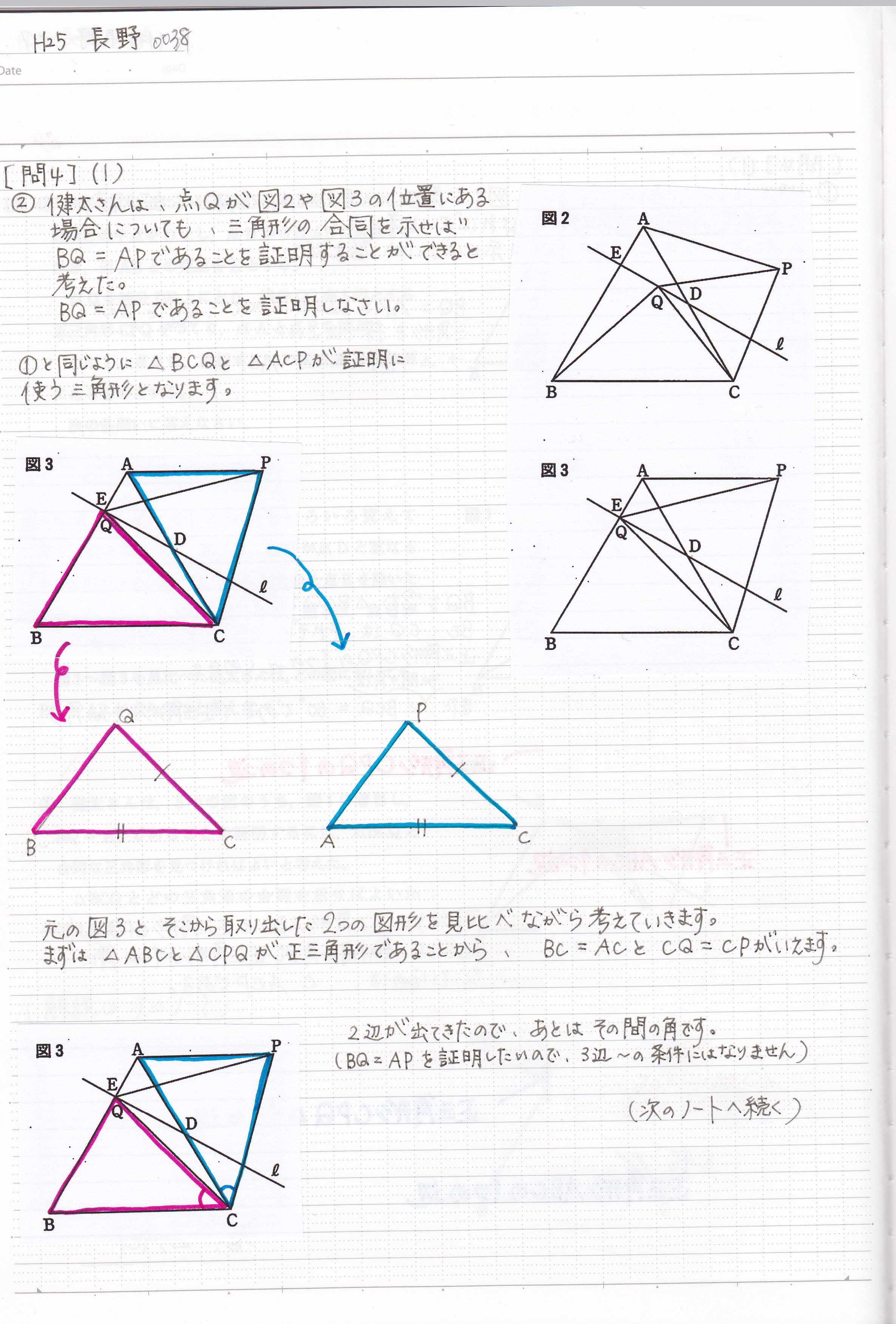



平成25年長野県立高校 入試問題 図形の証明問題 合同 現役塾講師のわかりやすい中学数学の解き方




数学 中3 46 相似の証明チャレンジ Lv 1 Youtube




これで点が取れる 単元末テスト中2数学 5章 図形の性質と証明




図形の証明問題です 全く分かりません 分かる方教えてください Clear



3




中学2年数学 図形の調べ方 図形と証明 確認問題7 あんのん塾




こわくない 数学 図形の証明問題 中学生 Kumon Shop




苦手な人が多い図形の証明問題を解くコツを解説 実は非常に簡単なんです 学習塾 Step By Step




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
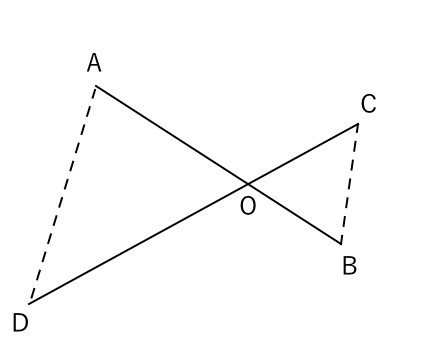



相似な図形 証明に慣れよう 苦手な数学を簡単に




三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学




メルカリ 中古理由あり 中学数学図形の証明がらくらく解ける 参考書 400 中古や未使用のフリマ



図形の証明のこれくらいの問題は自由記述でテストに出ますか 証明の問題は Yahoo 知恵袋




急ぎです W 中2の数学 図形の証明です Clear




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




図形に関する性質の証明 身勝手な主張




三角形の相似条件と証明問題の解き方 数学fun



中2数学 図形の証明 Eccジュニアbs小机教室 横浜港北区 子ども 大人英語英会話
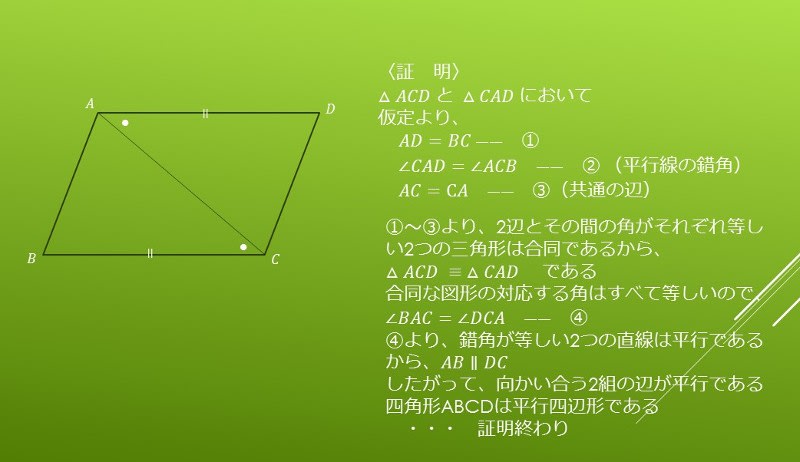



中2数学 図形の証明問題では様々な図形の性質を理解することが大切 中学生 受験対応 英語 数学 学習講座
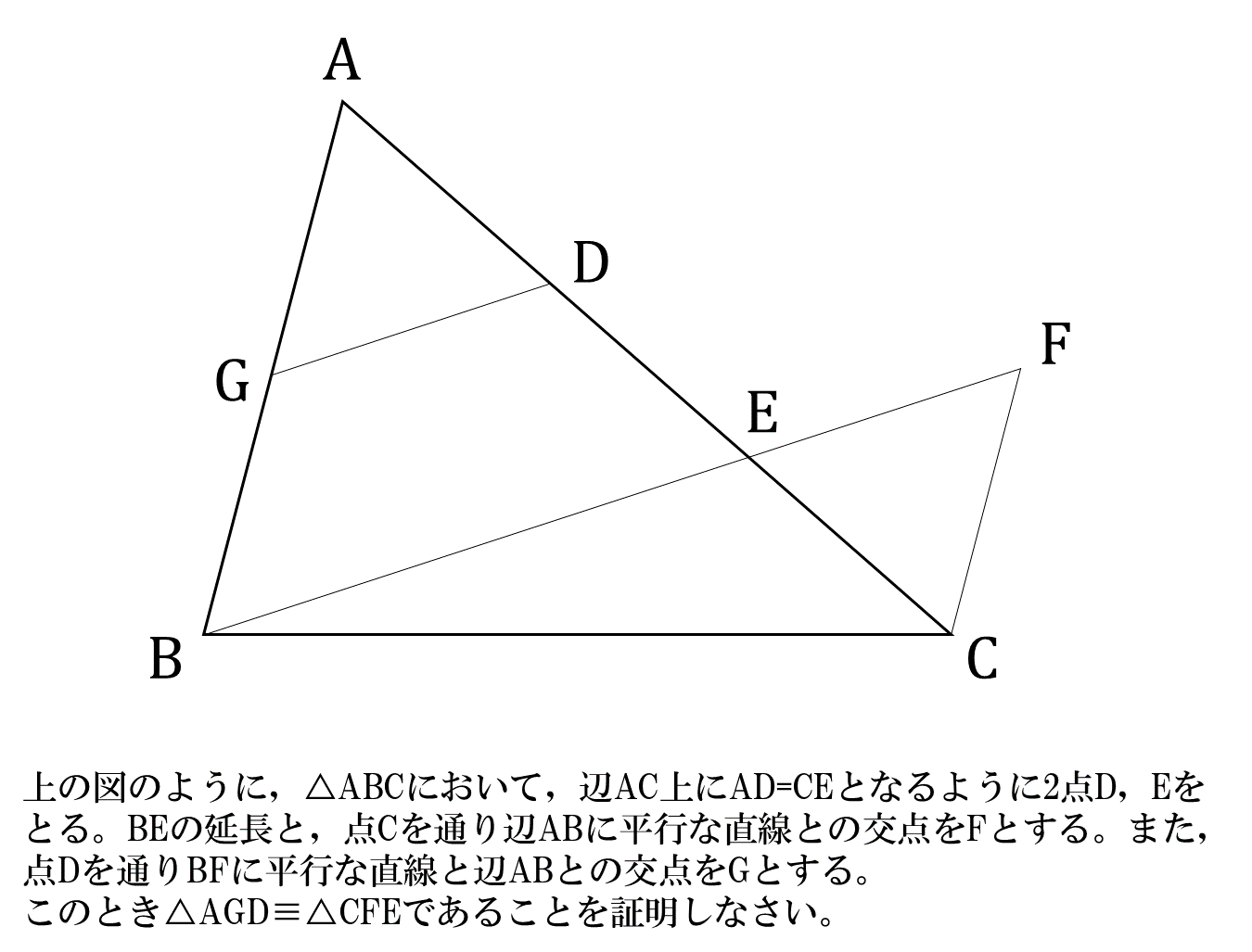



数学 中学証明問題を解く4つのポイント
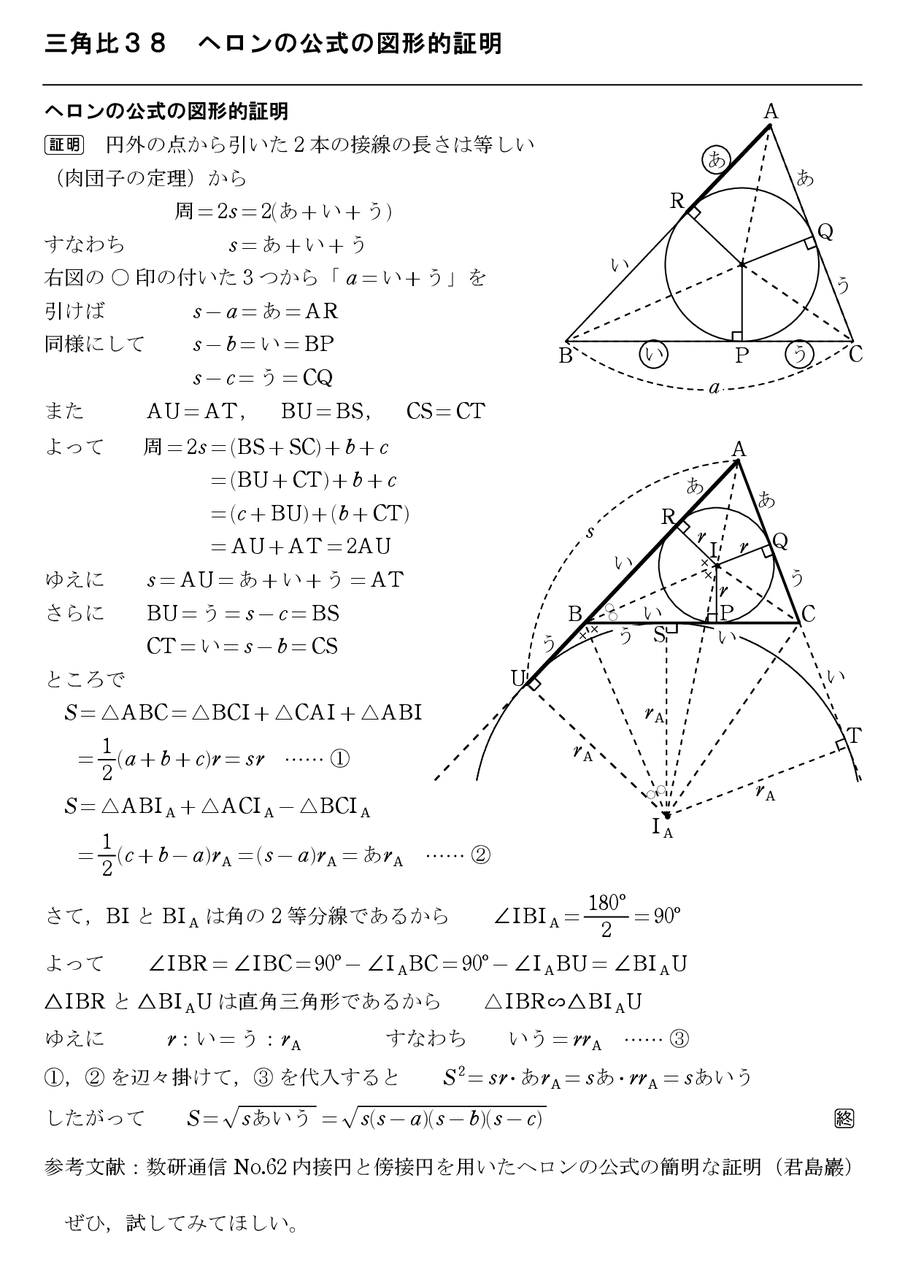



三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する
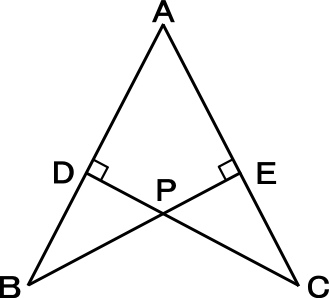



中学2年数学練習問題 図形と合同 三角形の合同の証明問題




超 パワーアップ中学数学 図形の証明 中継点 文字式の表現 活用テクニック Myisbn デザインエッグ社 長通 幸大 本 通販 Amazon




図形の証明はムズカシイ ニート戦記




図形に関する性質の証明 身勝手な主張
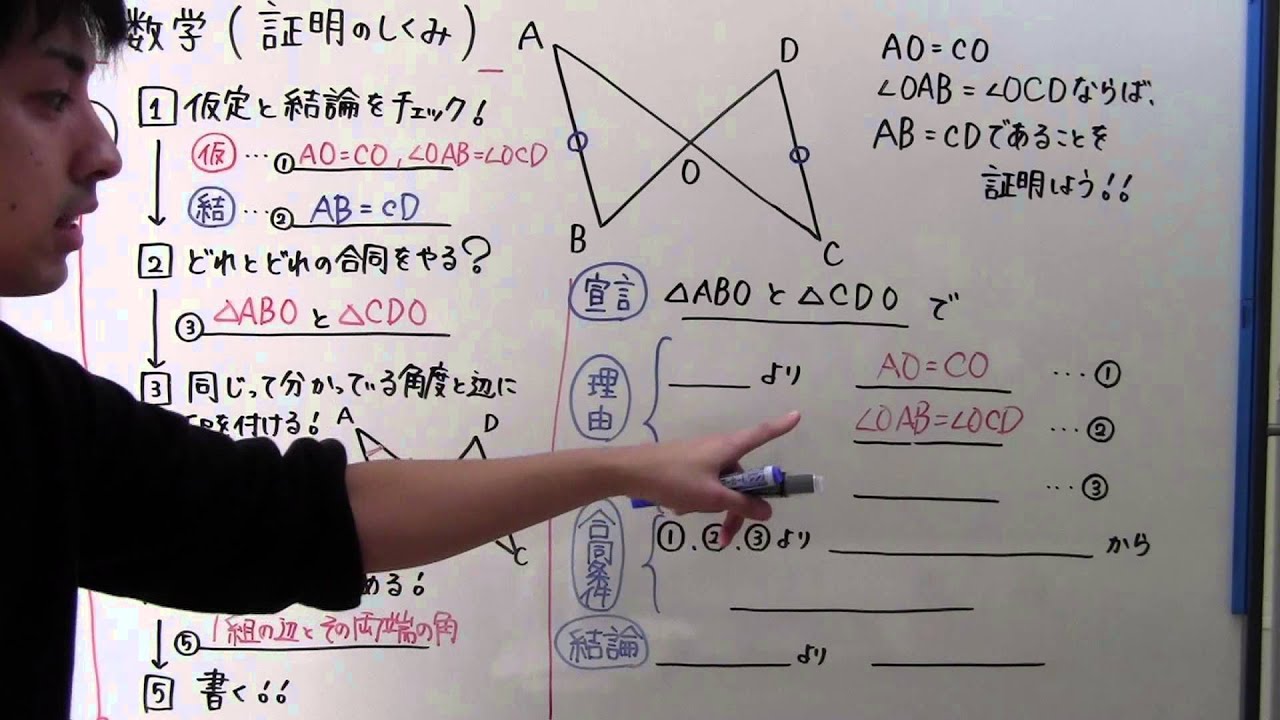



中2 数学 中2 60 証明のしくみ Youtube




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




2が無理数であることの図形的な証明 理系のための備忘録




1研究中 C 数学11 図形の証明 合同 相似 合同式 Mod余りの数 チェバの定理メネラウスの定理




直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
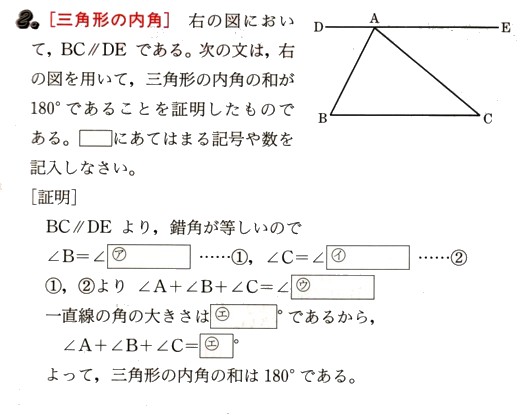



中学2年数学 図形の調べ方 図形と証明 練習問題2 あんのん塾
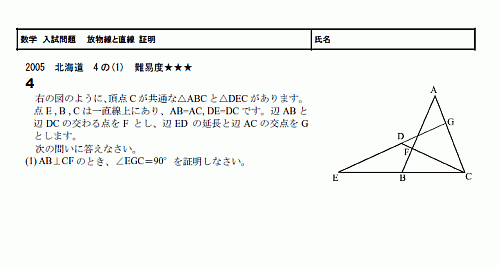



図形と証明 相似 スタディーx
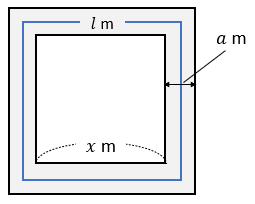



中3 式の計算の利用 円 正方形の図形の証明をイチから 数スタ




中2数学 証明とは 練習編 映像授業のtry It トライイット




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




中学生 合同な図形と証明のノート一覧 Clear




高校数学a 三角形の五心 三角形の内心とその存在証明 受験の月



0 件のコメント:
コメントを投稿